asymptoty trudne Krzysiek: cześć dosłownie za chwilę mam egzamin z matmy, jedne z typowych zadań to wyznacz asymptoty plus monotoniczność, wklęsłość itp mam takie przykłady i nie ogarniam tego w łatwiejszych jakoś szło ale przy trudniejszych, stoję ... prosiłbym kogoś o rozpisanie tych dwóch przykładów 1) f(x) = x−√x²−1 ] 2) f(x) = (x+2)*³√^x−2_x+2

Janek191: W środku nocy egzamin z matematyki ?

Kuba: Nie będę wszystkiego rozpisywał, ale mogę powiedzieć co po kolei. Wyznaczasz dziedzinę czyli x²−1≥0, jaki wynik?

Krzysiek: znam podstawy tylko trudności są z granicami jak mamy dziedzinę to (−∞,−1)u(1,∞) to jak sprawdzić czy ma pionowe asymptoty

Krzysiek: dosłownie za chwilę wtorek

Kuba: granica przy −1 z lewej strony i granica przy 1 z prawej

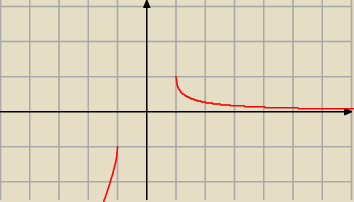
Janek191: D = ( − ∞, − 1> ∪ < 1, +∞ )

Janek191: f(−1) = − 1 i f(1) = 1 − nie trzeba liczyć granic. w − 1 i w 1.

Kuba: Janku, jak tutaj obliczyć ukośną w −∞? Wspł. kierunkowy wychodzi 0 i w takim wypadku b powinno wyjść niewłaściwe, ale nie mogę do tego dojść.

Janek191: Teraz policz pochodną .

Janek191:

f(x)
	= 1 − √1 − 1x2
x

	f(x)
lim		= 0
	x

x→−∞ Brak asymptoty ukośnej.

Krzysiek: w pierwszym policzyłem i porównuje do 0 z czego wychodzi że jest sprzeczność brak miejsc zerowych i co w takim wypadku ? a w drugim pochodna to meksyk

Kuba: Ale może być pozioma i jest w +∞, a chciałbym pokazać, że nie ma w −∞

Janek191: Jest asymptota pozioma lewostronna : y = 0 bo lim f(x) = 0 x→+∞

Janek191:

	2 x		x
f '(x) = 1 −		= 1 −
	2 √x2 − 1		√x2 −1

Dla x < − 1 f '(x) > 0 − f. rośnie od −∞ do −1. Dla x > 1 f '(x) < 0 − f. maleje od 1 do 0

Kuba: a nie prawostronna? Ale dalej nie wiem jak pokazać, że nie ma lewostronnej poziomej W sumie sprowadza się to do granicy z x−√x²−1 w −∞, ale właśnie z nią mam kłopot

Krzysiek: a ja nie rozumiem zapisu monotoniczności

Janek191:

	2 x   √x2 − 1 − x *   2√x2 − 1
f ''( x) = − (		) =
	x2 − 1

	x2 − 1 − x2		1
= − (		=		> 0 dla x z
	√ x2 − 1*(x2 − 1)		√x2 −1*(x2 − 1)

dziedziny. więc f jest wypukła w swojej dziedzinie.

Janek191: Monotoniczność − co tu do rozumienia ? Jeżeli f '(x) > 0 to funkcja rośnie, a jeżeli f '(x) < 0 to funkcja maleje.

Janek191: Co też potwierdza wykres danej funkcji.

Janek191: lim f(x) = − ∞ x→−∞

Janek191: ?

Krzysiek: inaczej rozwiązywałem takie zadania, nakładając miejsca zerowe y' i odczytując z wykresu a jak nie mam miejsc to się gubie

Krzysiek: jak szybko wyznaaczać te granice asymptoty − tak jak Janku Ty robisz że f(x)=x wtedy x jest asymptotą, jest poprawnie mogę tak na egzaminie robi c>

Janek191: Ale z wzoru na pochodną widać wyraźnie kiedy pochodna jest dodatnia, a kiedy ujemna. Oczywiście nie ma ekstremów, bo pochodna się nie zeruje.

Janek191:

	x2 − ( x2 −1)		1
f(x) = x − √x2 − 1 =		=
	x + √x2 − 1		x + √x2 − 1

więc

	1
lim f(x) =		= 0
	+∞

x→+∞

Janek191: Tutaj ( i w podobnych przykładach ) korzystamy z wzoru

	a2 − b2
a − b +
	a + b

Janek191:

	a2 − b2
a − b =
	a + b

Krzysiek: doobrze Janku dzięki za to a ten drugi przykład, dużo trudniejszy rachunkowo już jest obliczyłem pochodną ale nic nie umiem z niej wyczytać, a granice i asymptoty − kappa

Janek191: Jaki kierunek studiujesz ?

Janek191: Dzisiaj już nie mam siły.

	3√ x −2
f(x) = ( x + 2)*		?
	3√x + 2

Krzysiek: informatykę ale jestem po starym technikum i ciężko z matmą

Janek191: Ja też jestem po starym technikum − matura 1975.

Krzysiek: a z matematyką jaką masz styczność nachodzeń?

Janek191: Teraz tylko tutaj i czasem na korepetycjach z matematyki. Jestem emerytem.

Krzysiek: Nieodpowiednie określenie, 'emeryt' nie udziela się w takim stopniu na forum Miło że są tacy ludzie, którzy pomagają sami z siebie

Janek191: Emeryt oznacza zasłużony. Eta też jest bardzo aktywną emerytką i z jakimi pomysłami

Krzysiek: Tylko się cieszyć

5-latek: Janek191 Przeciez Eta to teraz 3LO

Krzysiek: W jakim mieście mieszka Eta?

Krzysiek: 9:21 pytanie od drugiego Krzyśka