Brzydko mi wychodzi ;/ Ewka: Dany jest trapez równoramienny o podstawach 4 i 9. Oblicz odległość pomiędzy środkami okręgu opisanego na tym trapezie i okręgu wpisanego w ten trapez.

Jack: ja chce rozwiazac, dajcie mi ; D

Eta: Ok

Mila:

Eta: Coś długo Ci to idzie Jacuś

Jack: Bo coś chyba nie idzie... obliczylem wiele niepotrzebnych rzeczy...jak zawsze

Mila: c=? r=? R=?

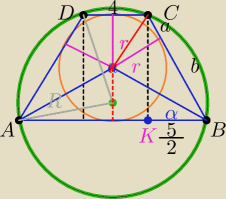
Jack: 2r = h_trapezu Z wlasnosci okregu wpisanego w czworokat : 4+9 = 2*(a+b) 13 = 2(a+b)

	13
a+b =
	2

ze sredniej geometrycznej (czy jakos tak) r² = a*b z ΔKBC :

	5
(a+b)2 = (		)2 + h2
	2

	13		5
(		)2 − (		)2 = h2
	2		2

	169−25		144
h 2 =		=
	4		4

	12
h =		= 6
	2

2r = 6 −>> r= 3 {r² = a*b = 9

	13		9
{a+b =		−−>>a = 2, b =
	2		2

	3		2
tg α =		=
	5   +2 2		3

	2		r
wtedy sin α =		=
	√13		R

	r √13		3
R =		=		√13
	2		2

Jack: bosz, ostatnie linijki z tym sinusem sie nie zgadzaja −.−, nie ten kat wzialem

Ewka: Fajny rysunek ja się bawiłam w wyznaczanie wzoru na R i padłam bo wychodziło jakieś 52879/144 czy coś takiego i nie moge tego R policzyć

Jack: dobra tam, ktos inny wykona to porzadniej xd

Jack: R mozna z tw. cosin.

	2
92 = 2R2 − 2 R2 cos (90 − alfa), gdzie tg alfa =		, więc cos alfa mozna znalez, tak
	3

samo cos 90 − alfa

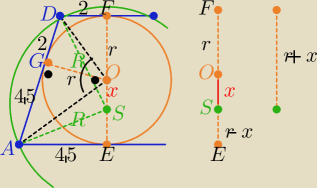
Eta: W ΔAOD : r²=2*4,5 ⇒ r=3 i |SE|=r−x , |FS|=r+x Z twierdzenia Pitagorasa w ΔASE i w ΔDFS R²=(r−x)²+(4,5)² R²= (r+x)²+2²

	65
to: (3+x)2−(3−x)2= 16,25 ⇒ 6*2x=16,25 ⇒ x=
	48

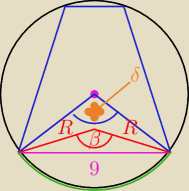
Jack: o kurcze, odwrotnie powiedzialem... β = 2δ (bo oparte na tym samym luku)... δ = 180 − 2α β = 360 − 4α a dobra ja sie juz lepiej nie wypowiadam...

Eta:

Eta: W taki trapez , który narysowałeś .... nie da się wpisać okręgu

Jack: w ten tu sie nie da,ale w ten wyzej czemu nie : D

Eta: Mówię o tym z 19:08

Jack: kurcze...nigdy nie wiem ktore dane mi sie przydadza...hmm nastepnym razem pomysle jak to zrobic niz obliczac wszystko i moze wyjdzie xd

Eta: A co powiesz na moje rozwiązanie?

Jack: proste...zbyt proste nikt tak prosto nie liczy !

Eta:

Jack: skad wiadomo ze |∡AOD| = 90 ?

Eta: Wykaż ................

Jack: podziekuje ; D

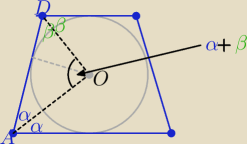
Eta: 2α+2β=180^o ⇒ α+β=90^o

Eta: Na zdrowie ........

Jack: nie bylo pytania

Jack: nie kojarzy mi sie to za dobrze z "na zdrowie"

Eta: To jedz kebab

Pomidor: Podczas porównania R² jest chyba błąd powinno być 12x=12,25 a nie 16,25 zgubiłaś 4 podczas obliczeń. 49/48 mi wyszlo.

Jack: 20,25 − 4 = 16,25?

Pomidor: Skąd się wzięło 20,25?

Eta: 4.5²=20,25 , 20,25−4= 16,25