Punkt przecięcia wykresów funkcji Ola: Dla jakich wartości parametru k punkt przecięcia wykresu funkcji y=2x+k−5 i y=3x−2k+1 leży wewnątrz kwadratu o wierzchołkach A=(0,0) B=(3,0) C=(3,3) D=(0,3).

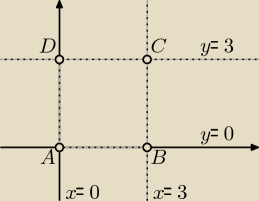
Bogdan: Trzeba najpierw z układu równań wyznaczyć x, y i potem rozwiązać układ nierówności: 0 < x < 3 0 < y < 3

Ola: Taki warunek napisałam właśnie, ale wychodzi mi jakaś bzdura. Zrobiłam to metodą wyznaczników. W=1 Wx=3k−6 −−> x Wy=7k−17 −−>y zapisałam później to tak : 0<x<3 0<y<3 0<3k−6<3 i 0<7k−17<3 wyszło : k€(2,3) i k€(2³₇,3) ale sprawdziłam że dla k = 3,5 i k =2 punkt przeciecia prostych dalej zawiera sie w tym kwadracie, wiec cos jest nie tak.

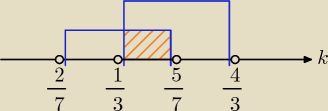
Bogdan: y = 2x + k i y = 3x − 2k + 1 2x + k = 3x − 2k + 1 ⇒ x = 3k − 1 i y = 2(3k − 1) + k = 7k − 2

	1		4
0 < 3k − 1 < 3 ⇒ 1 < 3k < 4 ⇒		< k <
	3		3

	2		5
0 < 7k − 2 < 3 ⇒ 2 < 7k < 5 ⇒		< k <
	7		7

	1		5
Odp.: k∊(		,		)
	3		7