Trudne zadanie tekstowe (pochodne) logarytm: Tekst w ksiażce zajmuje na kazdej stronie powierzchnie 300 cm2, marginesy z lewej i prawej strone sa równe 1; 5 cm, a marginesy z dołu i z góry sa równe 2 cm. Zaprojektowac wymiary kartek w tej ksiazce tak, aby zuzyc jak najmniej papieru. Mógłby ktoś dać chociaż jakiś pomysł jak zabrać się do tego zadania? Będzie to miało związek z pochodnymi, ponieważ mam to zadanie właśnie na liście z pochodnymi

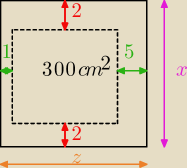
kochanus_niepospolitus: Hahaha ... zabawne zadanie. Ciekaw jestem, jak autor zadania chciałby spiąć książkę, jeżeli lewy margines ma zaledwie 1cm (przy 5cm prawego marginesu). i teraz co mamy: Dane: (x−4)*(z−6) = 300 cm² Funkcja: F(x,z) = x*z (szukasz minimum tej funkcji) Z 'danych' wyznacz zmienną 'z' (uzależnij ją od zmiennej 'x'). Mając to podstawiasz do funkcji F(x,z) i otrzymujesz funkcję jednej zmiennej 'f(x)'. Liczysz jej pochodną i rozwiązujesz zadanie.

logarytm: Mój błąd podczas przepisywania, powinno być 1,5cm, a nie 1;5cm Ale to niewiele zmieni, jedynie (x−4)*(z−3)=300cm². Wielkie dzięki!

logarytm: Podszedłem do tego zadania trochę inaczej. x*y=300, z tego wyprowadziłem y=300/x. Obliczyłem pochodną f(x)=(x+4)(y+3) i tą pochodną przyrównałem do 0, dzięki czemu uzyskałem x=20 lub x=−20 (to trzeba było odrzucić bo kartka nie może mieć ujemnych wymiarów). Podstawiłem pod x*y=300 i wyznaczyłem y=15. Jeszcze raz dzięki za wytłumaczenie mi tego zadania.

kochanus_niepospolitus: pamiętaj że wymiary kartki to będzie x+4 i y+3 czyli odpowiednio 24 i 18