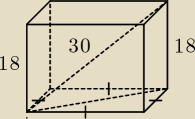
 Przekątna podstawy jest równa
302−182
co się równa 24 (√576)
Przekątna podstawy jest równa
302−182
co się równa 24 (√576)
| 24 | ||
czyli bok kwadratu jest równy | =8√3 | |
| √3 |
 Dzień dobry.
Kilka uwag do R.W.16l.
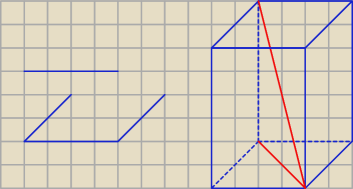
Rysunek nie przypomina graniastosłupa prawidłowego czworokątnego. Rysując położony
kwadrat postępujemy następująco − kreślimy poziomy odcinek o parzystej liczbie jednostek n,
(n jest liczbą, na pokazanym rysunku n = 4) (np. kratek w zeszycie), potem z obu końców
tego odcinka rysujemy pod kątem 45o (np. wzdłuż przekątnych kratek) odcinki równoległe,
każdy o długości n/2 (na rysunku n/2 = 2). Łączymy końce tych ukośnych odcinków otrzymując
obraz położonego kwadratu.
Przekątna jest lepiej widoczna, jeśli będzie poprowadzona tak, jak na tym rysunku.
Przekątna podstawy nie jest równa 302 − 182, ale jest równa √302 − 182 =
= √(30 − 18)(30 + 18) = √12 * 48 = √12 * 12 * 4 = 12 * 2 = 24.
Długość boku kwadratu nie równa się 8√3, tę długość obliczmy tak:
Dzień dobry.
Kilka uwag do R.W.16l.
Rysunek nie przypomina graniastosłupa prawidłowego czworokątnego. Rysując położony
kwadrat postępujemy następująco − kreślimy poziomy odcinek o parzystej liczbie jednostek n,
(n jest liczbą, na pokazanym rysunku n = 4) (np. kratek w zeszycie), potem z obu końców
tego odcinka rysujemy pod kątem 45o (np. wzdłuż przekątnych kratek) odcinki równoległe,
każdy o długości n/2 (na rysunku n/2 = 2). Łączymy końce tych ukośnych odcinków otrzymując
obraz położonego kwadratu.
Przekątna jest lepiej widoczna, jeśli będzie poprowadzona tak, jak na tym rysunku.
Przekątna podstawy nie jest równa 302 − 182, ale jest równa √302 − 182 =
= √(30 − 18)(30 + 18) = √12 * 48 = √12 * 12 * 4 = 12 * 2 = 24.
Długość boku kwadratu nie równa się 8√3, tę długość obliczmy tak:
| 24 | ||
a√2 = 24 ⇒ a = | = 12√2 | |
| √2 |
 doobra, będę uważniejszy na przyszłośc
doobra, będę uważniejszy na przyszłośc dzięki
dzięki 