Wyznacz esktrema, monotonicznosc, asymptoty funkcji KiwiNieLata: Witam! Chcę prosić was o pomoc w wykonaniu dwóch zadań związanych z granicami. 1. Wyznacz ekstrema, przedziały monotoniczności oraz asymptoty funkcji: y=x*√(x−1) 2. Wyznacz przedziały wklęsłości, wypukłości oraz punkty przecięć funkcji: y=2x/(1+x²)

Janek191: 1. y = x*√ x − 1 ?

	2 x
2. y =
	1 + x2

KiwiNieLata: Dokładnie tak

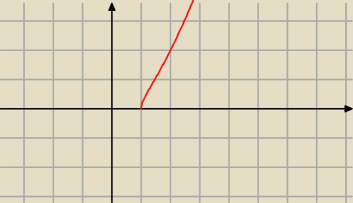
Janek191: z.1 x − 1 ≥ 0 ⇒ x ≥ 1

	1
y ' = 1*√x − 1 + x*		> 0
	2 √x − 1

więc funkcja jest rosnąca w swej dziedzinie. Brak ekstremów, brak asymptot.

KiwiNieLata: Przepraszam, ale w pierwszym przykladzie dopiero teraz zobaczylem pomylke...y=x*√1−x

Janek191: z. 2

	2 x
y =		D = ℛ
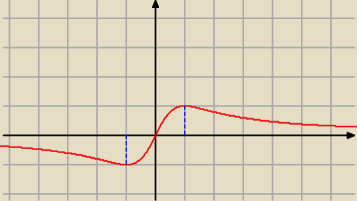
	1 + x2

więc

	2*( 1 + x2) − 2 x* 2x		2 − 2 x2
y ' =		=		= 0 ⇔
	( 1 + x2)2		( 1 + x2)2

⇔ 2 − 2 x² = 0 ⇔ x = − 1 lub x = 1

	( − 4 x*( 1 + x2)2 − ( 2 − 2 x2)*2*(1 + x2)*2x
y '' =
	( 1 + x2)4

Mamy y ''( − 1) > 0 − f. ma minimum lokalne dla x = − 1 y ''( 1) < 0 − f. ma maksimum lokalne Jednym z punktów przegięcia jest x = 0 bo y ''(0) = 0 Są jeszcze dwa.

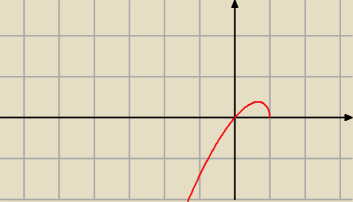
Janek191: y = x*√1 − x 1 − x ≥ 0 ⇒ 1 ≥ x ⇒ x ≤ 1

	1		2*(1 − x) − x
y ' = √1 − x − x*		=		=
	2 √1 − x		2 √1 − x

	2 −3 x		2
=		= 0 ⇔ x=
	2 √1 − x		3

	2
W x =		pochodna zmienia znak z + na − , więc funkcja ma maksimum lokalne.
	3

	2		2
Dla x <		funkcja rośnie, a dla x >		funkcja maleje.
	3		3

Brak asymptot.

KiwiNieLata: Dziękuję!