liczby zespolone madzik: Rozwiąż równanie: z⁶ + 2z³ + 2=0 Mam problem z takimi równaniami, gdzie ewidentnie widać, że trzeba zrobic podstawienie, tak jak w przykładzie powyżej. Jak takie przykłady rozwiązywać?

utem: z³=u u²+2u+2=0 Δ=4−8=−4=4i²

	−2−2i		−2+2i
u1=		lub u2=
	2		2

u₁=−1−i lub u₂=−1+i z³=−1−i lub z³=−1+i z=³√−1−i lub z=³√−1+i teraz wzory de Moivre'a Poradzisz sobie?

Janek191: z³ = t t² + 2 t + 2 = 0 Δ = 4 − 4*1*2 = − 4 = 4 i² √Δ = 2 i

	− 2 − 2 i		−2 + 2 i
t =		= − 1 − i lub t =		= − 1 + i
	2		2

zatem z³ = − 1 − i lub z³ = − 1 + i I teraz oblicz po trzy pierwiastki 3 stopnia ( z postaci trygonometrycznej ).

madzik: Tak, dalej już obliczę, dziękuję!

madzik: a jak teraz narysowac zbiór rozwiązań na płaszczyźnie zespolonej? Wyniki wyszły w postaci trygonometrycznej, której nie da się zamienić na postać kartezjańską

Mila: z³ = − 1 − i |−1−i|=√2

	5π
φ=
	4

	5π   +2kπ 4		5π   +2kπ 4
zk=3√√2*(cos		+i sin		), k=0,1,2
	3		3

	5π		5π
z0=6√2*(cos		+i sin		)
	12		12

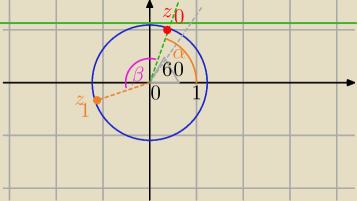
rysujesz okrąg o promieniu r=⁶√2≈...a rysunku zaznaczyłam z₀

	5π
α=		=75.
	12

z₁ na tym samym okręgu , β=120 ^o z₃ − znowu dodajesz 120^o. To samo robisz z drugim równaniem i zaczynasz od z₀, potem co 120⁰ następne pierwiastki.

madzik: Dziękuję ślicznie!

Mila: