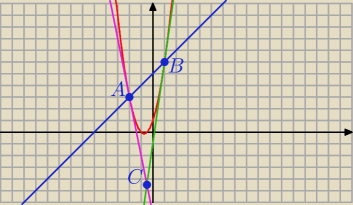
rach.rozniczkowy xyz: Parabolę y = 2x2+ 3x + 1 przecina prosta y = x + 5 w punktach A i B. Oblicz pole trójkąta ABC, gdzie C jest punktem wspólnym stycznych do paraboli w punktach A i B.

Jack: Fajne zadanie Podsraw do rownania paraboli y = x + 5 i otrzymasz 2 punkty...

xyz: 2x2+ 3x + 1 = x + 5 2x2+2x−4=0 a=2 b=2 c=−4 Δ=4−4*2*(−4) Δ=4+32 Δ=36 x1=1 x2=−2 Dobrze? O to chodzi ?I co dalej jeśli juz ?

Janek191: y ' = 4 x + 3 y '( − 2) = − 5 y = − 5 x + b A = ( − 2, 3) 3 = − 5*(−2) + b ⇒ b = − 7 y = − 5 x − 7 − prosta styczna w A. ======== y '( 1) = 7 y = 7 x + k B =( 1 , 6) 6 = 7*1 + k ⇒ k = − 1 y = 7 x − 1 − prosta styczna w B ======= Szukam punktu wspólnego stycznych − 5 x − 7 = 7 x − 1 − 12 x = 6

	1
x = −
	2

	1
y = − 4
	2

	1		1
C = ( −		; − 4		)
	2		2

===================

Janek191: → CA = [ −2 − (−0,5) ; 3 − (−4,5)] = [ −1,5 ; 7,5 ] → CB = [ 1 − (−0,5 ) ; 6 − ( − 4,5) ] = [ 1,5 ; 10,5 ] Pole Δ ABC → → P = 0,5 *I det ( CA , CB ) I = 0,5 *I −1,5*10,5 − 7,5 * 1, 5 I = = 0, 5 * I − 15,75 − 11,25 I = 0,5* 27 = 13,5 ===============================