proszę o pomoc xxxxx: Podstawa AB trójkąta równoramiennego ABC zawiera się w prostej o równaniu y=x+2 wierzchołek A=(−4,−2) , C=(2,−3). Oblicz pole tego trójkąta.

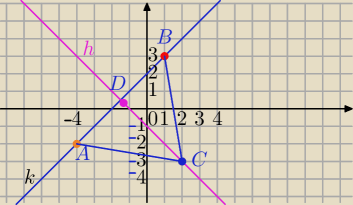
utem: AC− ramię ΔABC k: y=x+2 Wysokość opuszczona z punktu C dzieli podstawę na połowy i jest do niej prostpadła. h: y=−x+b i C∊h −3=−2+b⇔b=−1 h: y=−x−1 Wsp. punktu D

	3		3		1
x+2=−x−1⇔2x=−3 ⇔x=−		, y=−		+2=
	2		2		2

	3		1
D=(−		,
	2		2

k: x−y+2=0

	|2+3+2|		7
d(C,k)=		=
	√12+12		√2

	7√2
|CD|=
	2

|AD|=√((−1.5+4)²+(0.5+2)²=√6.25+6.25=√6.25*2=2,5√2

	7√2
PΔ=2.5√2*		=17.5
	2

B=(1,3)