Wyznacz asymptoty funkcji Ania: Wyznacz asymptoty funkcji f(x)= ^x2+1_x−1

Janek191: x ≠ 1

f(x)		x2 + 1
	=
x		x2 + x

	1   1 +   x2
lim		= 1 = a
	1   1 +   x

x→+∞ oraz

	x2 + 1		x2 + 1 − ( x2 − x)
lim (		− x) = lim (		) =
	x − 1		x − 1

x→ +∞ x→+∞

	x + 1
= lim		= 1
	x − 1

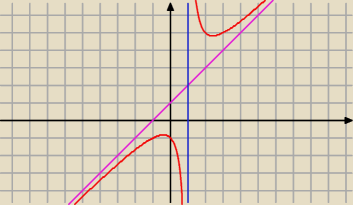
x→+∞ y = a x + b = x + 1 − asymptota ukośna oraz x = 1 − asymptota pionowa.

Janek191: Tam jest pomyłka. Powinno być

f(x)		x2 + 1
	=		→ 1, gdy x→+∞
x		x2 − x

Metis: Janku badasz tylko +∞? Jak rozpoznać, że nie potrzeba badania w −∞ ?

Janek191:

	f(x)
lim		= 1
	x

x→ −∞

Jack: Hmmm a to chyba sie nie da by byly dwie asymptoty ukosne...? Jedna minus x a druga x. Bo wtedy liczac poziome bysmy musieli miec wynik granicy jako 2 wyniki...

Jack: I tak wlasciwie nie wystarczy badac jednego przypadku? Jesli jest w nieskonczonosci to znaczy ze jest... A jak nie to nie... Bo czy badamy w + czy w − ∞ to jwst ta sama asymptota...

Metis: Nie. Mogą być różne. http://prntscr.com/9vx318

Janek191: I wszystko jasne

Metis: Mój profesor zawsze wiedział, czy liczyć w +∞ czy w −∞, nie wiem czy wynikało to z jego wprawy, czy też patrzy się "na coś", czego nie wiem, stąd pytanie

Jack: No coz...ja nie spotkalem przypadku gdzie bym mial 2 asymptoty ukosne

Jack: A co do tego linku...jesli policzymy granice i wychodzi konkretna liczba no to czy plus czy minus nieskonczonosc granica bedzie ta sama...

Metis: No własnie rzecz w tym, że w zależności czy liczymy granice w +∞ / −∞ granice mogą wyjść inne

piotr1973: funkcja f(x)= x− arctgx ma asymptoty ukośne: y=x−π/2 w +∞ y=x+π/2 w −∞

Jack: Na poziomie licealnym raczej watpie xd

tes: z tym arctg najbardziej klasyczny przykład chyba.