Monotoniczność Kamil: Mam pytanie czy dla funkcji f=x*e⁻x funkcja rośnie w przedziale od (0,2) maleje w przedziale (−∞,0) U (2,∞) A minimum osiąga w punkcie 0 a maksimum w punkcie 2, czy coś źle policzyłem?

Kamil: Sorki ma być f=x*e^−x

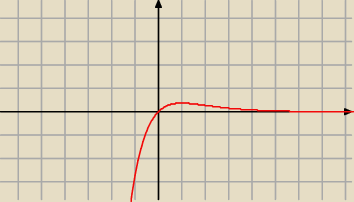
Janek191: Ma być f(x) = x*e^−x Źle policzone. To zadanie było już kilka razy rozwiązywane w ostatnim czasie.

Janek191: Policz pochodną tej funkcji.

Kamil: Przepraszam źle to zapisałem miało być x²*e^−x tutaj pochodna mi wychodzi e^−x (2x−x²) dobrze?

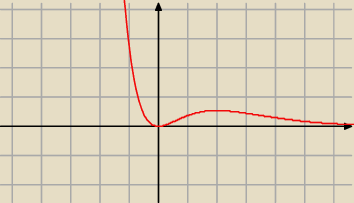
Janek191: f(x) = x²*e^−x f '(x) = 2 x*e^−x + x²*e^−x*(−1) = e^−x*( 2 x − x²) = 0 ⇔ x = 0 lub x = 2

Kamil: funkcja rośnie w przedziale od (0,2) maleje w przedziale (−∞,0) U (2,∞) dobrze to w takim razie napisalem?

Janek191: Tak Lepiej zapisać: f maleje w przedziałach: ( − ∞, 0) , ( 2, +∞)

	1		1
W sumie nie maleje, bo np. f(−		} < f( 2		)
	4		4