Zbadaj, jakie relacje inkluzji zachodza pomiedzy zbiorami ALE: Zbadaj, jakie relacje inkluzji zachodza pomiedzy zbiorami A,B i C, jesli: (A∩B) \ (B\C) = A∩C Miałem taki przykład na lekcji i do tego momentu rozumiem p= x∊A q= x∊B z= x∊C "((p⋁q)⋀ ¬(q∧¬z))<=>(p⋀z))" ale potem okazuje się, że jest jeszcze taka imiplikacja na końcu "=>(p=>(z∨q))" i całość wygląda tak ((p⋁q)⋀ ¬(q∧¬z))<=>(p⋀z))=>(p=>(z∨q)) Skąd to się bierze?

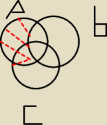
ALE: Wychodzi na to, że można to niby zauważyć z diagramu Venna, ale nie rozumiem, czemu wyszła taka zależność przecież jak narysujemy sobie (A∪B)\(B\C) to wyjdzie nam coś takiego