Wyznacz równanie stycznej do wykresu funkcji f, w podanym punkcie. kindziorek643: Wyznacz równanie stycznej do wykresu funkcji f, w punkcie P ( x0, 0): f(x)= 2ln(x² − √ex + √e³) −3 Mam spory problem z wyznaczeniem tutaj dziedziny, przez co również potem i x0, ponieważ wychodzą mi dwa wyniki i nie jestem w stanie stwierdzić, który z nich będzie "wpadał" do dziedziny, a który nie. Będę wdzięczna za każdą pomoc

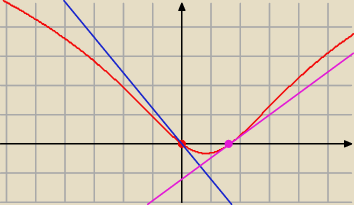
piotr1973: x² − e^1/2x + e^3/2>0 ⇒ x∊R x0 z równania 2*ln(x² − e^1/2x + e^3/2)−3=0 x0=0 lub x0=√e będą więc dwie styczne:

	2
w x0=0 y=−		x
	e

	2		2
w x0=√e y =		x−
	e		√e

Janek191: x² − √e x + e√e > 0 Δ = e − 4*1*e√e = e − 4e√e < 0 ⇒ x² − √e x + e√e > 0 dla x ∊ℛ x² −√e x + e√e = 1 x² − √e x + e√e − 1 = 0 Δ₁ = e − 4*( e√e − 1) = e − 4 e√e + 4 < 0 więc x² − √e x + e√e− 1 > 0 dla x∊ℛ Df = ℛ x_o = 0, bo f(0) = 0 czyli P = ( 0, 0)

	2x − √e
f '(x) = 2*
	x2 − √e x + e√e

zatem

	−2*√e		− 2
f ' (0) =		=
	e√e		e

y = a x + b

	2
y = −		x + b
	√e

0 = b

	2
. y = −		x
	√e

============= II x₀ = √e , bo f( √e) = 0 Wtedy P = ( √e , 0 )

	2√e −√e		2√e		2
f '( √e) = 2*		=		=
	e − e + e√e		e√e		e

	2
y =		x + b
	e

	2		2
0 =		*√e + b ⇒ b = −
	e		√e

	2		2
Odp. y =		x −		− wykres koloru fioletowego
	e		√e

=================

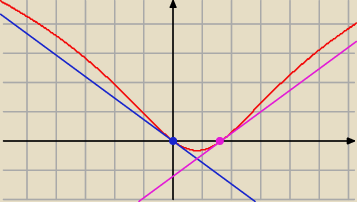
Janek191: Zauważyłem teraz, że była pomyłka przy zapisywaniu I prostej.

	−2
Oczywiście powinno być: y =		x
	e

Janek191:

kindziorek643: @Janek191 A mam jeszcze jedno pytanie. Obliczając Δ1 przyrównałeś liczbę logarytmowaną do 1. Skąd to się wzięło?

Janek191: Ten fragment rozwiązania jest niepotrzebny, Należy pominąć wiersze : 3 , 4.i 5.

kindziorek643: Ok, bardzo dziękuję za pomoc