Rozwiąż równanie-szereg+tryg. oolaaaja: Rozwiąż równanie−szereg+tryg. sin²x+sin³x+sin⁴x+...=1+sinx Jak na razie mam coś takiego

	sin3x
q=		=sinx
	sin2x

	a1		sin2x
S=		=
	1−q		1−sinx

Teraz przyrównałem

sin2x
	=1+sinx
1−sinx

sin²x=(1−sinx)(1+sinx) sin²x=1−sin²x 2sin²x=1 /:2

	1
sin2x=
	2

I co teraz? Bo jak opuszczam potęgę, to mi na końcu wychodzi zły wynik i nie wiem, jak sobie z tym poradzić

Janek191:

	1		1
sin x = −		lub sin x =
	√2		√2

oolaaaja:

	√2		√2
no i z tego sinx=		v sinx= −
	2		2

	√π		√π
xo=		v xo=−
	4		4

	√π		√π
x=		+2kπ v x= −		+2kπ
	4		4

	π
i co teraz? Bo potem sprawdzam zbieżność i wychodzi, że tylko x=		pasuję, a wynik to
	4

	π		π		π
x=		+k		. No i skąd to k		?
	4		2		2

Jack: √π skad to ; d

oolaaaja: Sorki, bez tego pierwiastka Poprawa:

	π		π
xo=		v xo=−
	4		4

	π		π
x=		+2kπ v x=−		+2kπ
	4		4

Jack:

	√2		√2
sin x =		lub sinx = −
	2		2

	π		3
x =		+ 2k π lub x =		π + 2kπ
	4		4

Jack: łe jeny, ale skopalem ...tak powinno byc :

	√2
sin x =
	2

	π		3
x =		+ 2kπ lub x =		π + 2kπ
	4		4

	√2
sin x = −
	2

	π		5
x = −		+ 2kπ lub x =		π + 2kπ
	4		4

po zaznaczeniu rozwiazan na osi mozna zauwazyc ze sie co jakis czas powtarzaja

Jack: bo mamy :

	π		π		3		5
−		,		,		π ,		π
	4		4		4		4

	2π		π
widac ze powstaja poprzez dodanie		czyli
	4		2

więc do odpowiedzi − bierzemy jakikolwiek wynik, np.

π		π		kπ
	i musimy dodawac krotnosci		czyli inaczej
4		2		2

więc ostateczna odp.

π		kπ
	+
4		2

Jack: oczywiscie mozesz zostawic w formie 4 wynikow... nikt nie powinien miec nic przeciwko

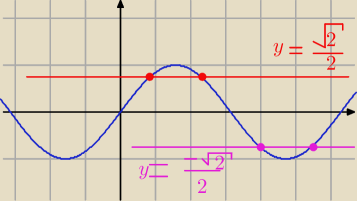Jack: bo Ty napisales tylko 2 wyniki mozliwe, a powinny byc 4

oolaaaja: Aaa, teraz wszystko rozumiem. Trochę nie robiłem zadania z tryg. i się zapomniało co nieco Dziękuję bardzo za pomoc!