ekstrema lokalne i przedziały monotonicznosci Julka: X³−X potrzebuję wyznaczyć miejsca zerowe, ekstrema min i max, wypukłości i monotonicznosci przedziały,oraz punkt albo punkty przegięcia wykresu funkcji. Proszę o wyjaśnienie krok po kroku co i jak mam liczyć, bo sama nie potrafię. miejsca zerowe z pochodnej wychodzą mi inne niż jak wyłączę X przed nawias i przyrównam do 0 nie wiem jak mam sie za to zabrać,

Janek191: A gdzie jest ta funkcja ?

Julka: f(x) = X³ − x

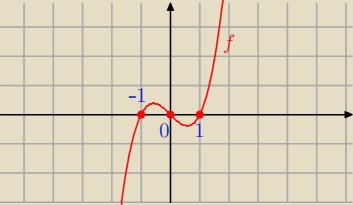
Janek191: f(x) = x³ − x

Janek191: Miejsca zerowe: f(x) = 0 ⇔ x*(x² − 1) = x *(x − 1)*(x + 1) = 0 ⇔ x = − 1 lub x = 0 lub x = 1

Janek191: Pochodna

	1		1		1
f '(x) = 3 x2 − 1 = 0 ⇔ 3 x2 = 1 ⇔ x2 =		⇔ x = −		lub x =
	3		√3		√3

II pochodna f '' (x) = 6 x zatem f ''( −U{√1[√3}) < 0 − funkcja w tym punkcie ma maksimum lokalne

	1
równe f( −		) =
	√3

	1
f ''(		) > 0 − funkcja w tym punkcie ma minimum lokalne
	√3

	1
równe f (		)
	√3

f '' (x) = 0 ⇔ x = 0 − punkt przegięcia Dla x < 0 jest f '' (x) < 0 − funkcja f jest wklęsła Dla x > 0 jest f '' (x) > 0 − funkcja f jest wypukła

Janek191: ?