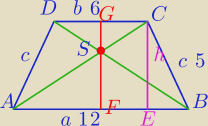
 1) W trapezie równoramiennym ABCD dane są |AB|=12, |CD|= 6, |AD|=|BC|=5. Przekątne trapezu
przecinają się w punkcie S. Oblicz pole trójkąta ABS.
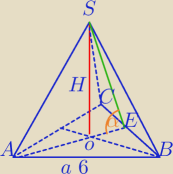
2) W ostrosłupie prawidłowym trójkątnym tangens kata nachylenia ściany bocznej do płaszczyzny
podstawy jest równy 3√2. Oblicz objętość ostrosłupa, wiedząc, że krawędź podstawy ma długość
6.
3) Liczby a, b, c są długościami boków trójkata. Pokazać, że a2 + b2 + c2 < 2(b+c)2
4) W pewnej 30−osobowej klasie uczniowie mogą wybrać zajęcia dodatkowe z malarstwa lub
fotografii. Wiadomo, że każdy z uczniów wybrał co najmniej jedne z zaproponowanych zajęć .
Prawdopodobieństwo tego, że losowo wybrana osoba z tej klasy uczęszcze na oba zajęcia wynosi
1/3. Natomiast prawdopodobieństwo tego, że losowo wybrana osoba z tej klasy uczęszcza tylko na
zajęcia z malarstwa wynosi 1/6. Ile osób wybrało zajęcia z malarstwa, a ile z fotografii?
Z góry dziękuję. Zrobiłbym sam, ale dopiero nadrabiam zaległości po wymuszonej przerwie w
szkolnych zajęciach i się nie wyrobię z tym sam do jutra
1) W trapezie równoramiennym ABCD dane są |AB|=12, |CD|= 6, |AD|=|BC|=5. Przekątne trapezu
przecinają się w punkcie S. Oblicz pole trójkąta ABS.
2) W ostrosłupie prawidłowym trójkątnym tangens kata nachylenia ściany bocznej do płaszczyzny
podstawy jest równy 3√2. Oblicz objętość ostrosłupa, wiedząc, że krawędź podstawy ma długość
6.
3) Liczby a, b, c są długościami boków trójkata. Pokazać, że a2 + b2 + c2 < 2(b+c)2
4) W pewnej 30−osobowej klasie uczniowie mogą wybrać zajęcia dodatkowe z malarstwa lub
fotografii. Wiadomo, że każdy z uczniów wybrał co najmniej jedne z zaproponowanych zajęć .
Prawdopodobieństwo tego, że losowo wybrana osoba z tej klasy uczęszcze na oba zajęcia wynosi
1/3. Natomiast prawdopodobieństwo tego, że losowo wybrana osoba z tej klasy uczęszcza tylko na
zajęcia z malarstwa wynosi 1/6. Ile osób wybrało zajęcia z malarstwa, a ile z fotografii?
Z góry dziękuję. Zrobiłbym sam, ale dopiero nadrabiam zaległości po wymuszonej przerwie w
szkolnych zajęciach i się nie wyrobię z tym sam do jutra
| 12 | ||
K = | = 2 | |
| 6 |
 1)
1)
| 12 | 2 | |||
ΔABS∼ΔDCS cecha kkk w skali k= | = | |||
| 6 | 1 |
| 4 | ||
x= | ||
| 3 |
| 8 | ||
|SF|=2x= | ||
| 3 |
| 1 | 8 | |||
PΔABS= | *12* | =16 | ||
| 2 | 3 |

 tgα=3√2
tgα=3√2
| 1 | ||
V= | *PΔABC*H | |
| 3 |
| 62√3 | ||
PΔABC= | ||
| 4 |
| a√3 | 6√3 | |||
|AE|= | = | =3√3 | ||
| 2 | 2 |
| 1 | ||
|OE|= | |AE|=√3 | |
| 3 |
| H | H | |||
tgα= | ⇔ | =3√2 | ||
| |OE| | √3 |

