 Współrzędne (p,q) spełniają układ warunków :
1/ Δ>0
i
2/ x12 +x22 =2
1/ Δ= 4p2 −4q => 4p2 −4q >0 => p2 −q >0
2/
x12+x22=(x1+x+2)2−2*x1*x2 =(−ba)2−2*ca=2 −−− ze wzorów Viete'a
to:
4p2 −2q= 2 => 2p2−q=1 => q= 2p2 −1
z 1/ p2 − 2p2 +1 >0 => p2 −1<0 => ( p−1)(p+1) <0 => p€( −1,1)
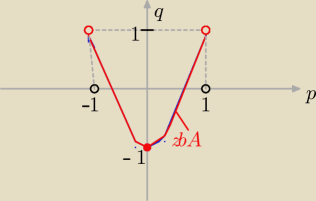
zatem zb.A ={(p,q): q= 2p2 −1 dla p€(−1,1) i p,q€R }
Zbiór A jest zbiorem takich punktów (p,q) ,które należą
do części paraboli q= 2p2 −1 dla p€ (−1,1)
Współrzędne (p,q) spełniają układ warunków :
1/ Δ>0
i
2/ x12 +x22 =2
1/ Δ= 4p2 −4q => 4p2 −4q >0 => p2 −q >0
2/
x12+x22=(x1+x+2)2−2*x1*x2 =(−ba)2−2*ca=2 −−− ze wzorów Viete'a
to:
4p2 −2q= 2 => 2p2−q=1 => q= 2p2 −1
z 1/ p2 − 2p2 +1 >0 => p2 −1<0 => ( p−1)(p+1) <0 => p€( −1,1)
zatem zb.A ={(p,q): q= 2p2 −1 dla p€(−1,1) i p,q€R }
Zbiór A jest zbiorem takich punktów (p,q) ,które należą
do części paraboli q= 2p2 −1 dla p€ (−1,1)
 ΩΔ
ΩΔ