Pochodne.
Infinity: | | (x+1) | |
Funkcja wymierna f jest dana wzorem f(x)= |
| . Wyznacz wartość najmniejszą i |
| | x2+2x+2 | |
największą, jakie ta funkcja przyjmuje dla argumentów z przedziału <−3,1>.
26 sty 21:08
Janek191:
Oblicz minimum oraz maksimum tej funkcji.
26 sty 21:12
Adam: x2 + 2x+ 2 ≠ 0 ⇒ Δ = − 4 ⇒ x ∊ R
f(−3) = −25
f(1) = 25
f'(x) = (x+1)'(x2+2x+2) − (x+1)(x2+2x+2)'(x2+2x+2)2
f'(x) = −x2 − 2x(x2+2x+2)2
Punkty podejrzane o ekstremum, gdy f'(x) = 0 ⇔ −x2 − 2x = 0
x = 0 ⋁ x = −2
f(0) = 12 → jest to wartość największa funkcji w przedziale <−3; 1>
f(2) = −12 → jest to wartość najmniejsza funkcji w przedziale <−3; 1>
26 sty 21:29
Adam: Przepraszam, za nieczytelne rozwiązanie, ale z powodu niewiedzy, zamiast "U" konsekwentnie
pisałem "u". Dlatego też ułamki wyglądają, tak jak wyglądają.
26 sty 21:31
Janek191:
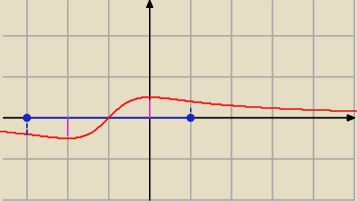
26 sty 21:32
mephisto: 2 nie należy do przedzialu podanego w treści wiec f(−3) bedzie miec najmniejszą wartość
1 maj 15:40
mephisto: nie ważne nie zauważyłam minusa
1 maj 15:43
