Zadania optymalizacyjne. Graniastosłup prawidłowy trójkątny Paulina: Wśród wszystkich graniastosłupów prawidłowych trójkątnych, w których suma wszystkich krawędzi jest równa 12, jest taki, który ma największą objętość. Oblicz długości krawędzi tego graniastosłupa.

Bogdan: Suma czego? Co to znaczy "suma wszystkich krawędzi"? to brzmi jak np. suma wszystkich jabłek − niejasne

Jack: 6a + 3h = 12 2a + h = 4 nic wiecej chyba z tego nie zrobie

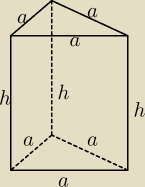
Mila: 6a+3h=12 3h=12−6a /:3 h=4−2a 4−2a>0⇔a∊(0,2)

	a2√3		a2√3
V(a)=		*(4−2a)=		*2*(2−a)
	4		4

	√3
V(a)=		*(2a2−a3)
	2

	√3
V'(a)=		*(4a−3a2)
	2

V'(a)=0⇔4a−3a²==0 a*(4−3a)=0 a=0∉D lub 3a=4

	4
a=
	3

	4
h=4−2*
	3

===========

Bogdan: Co Milu zrozumialaś w zapisie "suma wszystkich krawędzi"?, czy chodzi o sumę długości wszystkich krawędzi? ale o długościach nie ma slowa w poleceniu.

Eta: