123 TMS: wyznacz ekstrema funkcji

	x2
f(x)=
	x2−1

oblicza się pochodną i przyrównuje do 0 ?

TMS: ?

Janek191: Warunek konieczny istnienia ekstremum w x₀: f '(x₀)=0

TMS: wyszło mi rosnąca: (0:1)u(1:+∞) malejąca(−∞:−1)u(−1:0) mógłbyś sprawdzić ?

ICSP: x ∊ R \{−1 , 1}

	1
f(x) = 1 +
	x2 − 1

	−2x
f'(x) =		= 0 ⇒ x = 0 i w punkcie x = 0 mamy maksimum lokalne równe 0.
	(x2 − 1)2

f_↗ dla x ∊ (− ∞ ; −1) ∪ (−1 ; 0) f_↘ dla x ∊ (0 ; 1) ∪ (1 ; + ∞)

TMS: dziękuje bardzo odwrotnie parabole narysowałem

TMS: Jak będzie wyglądał wykres tej funkcji ?

TMS: x² to chyba ramiona do góry czy to nie ta funkcja bd rysowana ?

Jack:

	2x
f'(x) = −
	(x2−1)2

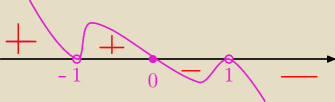
−2x(x²−1)² = 0 jak narysujesz... ekstremum : f_max(0) = ...

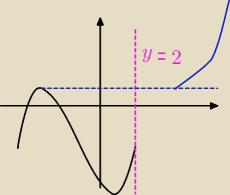
Jack: @ICSP mnie uczyli ze zapis f↗ dla x∊ (...) U (...) jest jak najbardziej bledny (na maturze 0pkt.) poniewaz funkcji nie rosnie jakby w sumie przedzialow...tylko rosnie , potem maleje i potem rosnie a z tego by wynikalo ze rosnie od tamtego gdzie skonczylo i np. tak jak na rysunku zrobilem to ten zapis jest bledny, bo jakby ona rosla, to by musiala rosnac tak jak (kolor niebieski) czyli wyzej jak wczesniej...a skoro rosnie, ale jest nizej jak poprzednio to tak srednio pasuje...

Jack: byc moze sie myle... ale mnie tak uczono