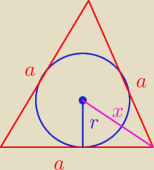
ostrosłup Roxi: W ostrosłupie prawidłowym trójkątnym promień okręgu wpisanego w podstawę jest równy 4√3 cm, a krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem 45 stopni. Oblicz pole powierzchni całkowitej i objętość tego ostrosłupa.

Janek191:

	1
r =		h
	3

h = 3 r = 12√3

	a√3
h =		= 12 √3
	2

a = 24 ===== x² = r² + 12² = 16*3 + 144 = 192 = 64*3 x = 8√3 α = 45^o więc h = x = 8√3 − wysokość ostrosłupa h₁² = r² + h² = 48 + 192 = 240 = 16*15 h₁ = 4√15 − wysokość ściany bocznej

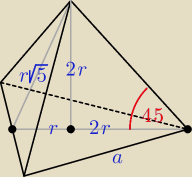
Bogdan: r = 4√3

1
	a√3 = r /*2√3 ⇒ a = r*2√3
6

dero2005: r = 4√3 = ¹₃h_p h_p =. → wysokość podstawy a = ²₃h_p√3 =. → krawędź podstawy

	a2√3
Pp =		=. →pole podstawy
	4

h → wysokość ostrosłupa

h
	= tg45o = 1
2   hp 3

h = h_s. → wysokość ściany bocznej h_s = √h² + (¹₃h_p)² =

	1
V =		Pp*h =. Objętość
	3

	a2√3		3
Pc =		+		a*hs =. pole całkowite
	4		2

Janek191:

	a2√3
Pc = Pp + Pb =		+ 3*0,5 a*h1 = 144√3 + 144√15 [ cm2]
	4

	1		1
V =		Pp*h =		*144√3*4√15 = 192√45 = 192*3√5 = 576√5 [ cm3]
	3		3