geometria analityczna naileo: Wyznacz współrzędne punktu przecięcia symetralnych trójkąta ABC. Korzystając z tego, że punkt ten jest równo odległy od wierzchołków trójkąta, podaj równanie okręgu opisanego na trójkącie ABC. a) A(0,0), B(4,−4), C(4,8) b) A(−2,−2), B(6,−2), C(2,6) Z jakiegoś powodu w układzie równań mi nie wychodzi, gdzieś popełniam błąd, zarówno w przykładzie a i b. Bardzo proszę o rozwiązanie krok po kroku powyższego zadania.

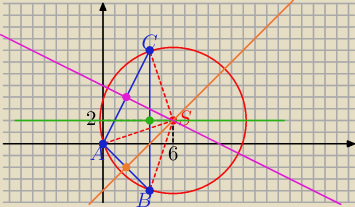
Eta: a) środek boku BC : (4,2) symetralna boku AC : y=2 środek boku AB : (2,−2) wsp. kier prostej AB : a_AB=−1 to symetralna boku AB : y= 1(x−2)−2 ⇒ y= x−4 y=2 to x−4=2 ⇒ x=6 zatem S(6,2) i R²= |AS|²= 40 o : (x−6)²+(y−2)²=40 b) podobnie