Całki Marcin: ∫tgxdx

Mila:

	sinx
=∫		dx= ?
	cosx

Marcin: i co dalej ?

Mila: [cosx=t, −sinx dx=dt]

Marcin: a jesteś dobra z wyznaczania monotoniczności ?

Marcin: bo potrzebował bym monotnoniczność z f(x)= 2x² / (x−1)²

kyrtap: widzę że ktoś tutaj lenia ma

Mila: D=R\{1} 1) x=1 asymptota pionowa 2)pochodna f(x)

	4x*(x−1)2−2x2*2*(x−1)*1
f'(x)=
	(x−1)4

	4x*(x−1)2−4x2*(x−1)
f'(x)=		=U{(x−1)*(4x*(x−1)−4x2}=
	(x−1)4

	(x−1)*(−4x		−4x
=		=
	(x−1)4		(x−1)3

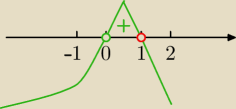
3) Ekstrema f'(x)=0 ⇔x=0 kandydat. 4) Monotoniczność f'(x)>0 −4x*(x−1)³>0 x∊(0,1) f(x) rosnąca dla x∊(0,1) dla x∊(−∞,0)∪(1,∞) funkcja f(x) jest malejąca w tych przedziałach 5) w x=0 ma maksimum lokalne , pochodna zmienia znak z (−) na (+) przy przejściu przez x=0) f(0)=0 Teraz licz granice na krańcach dziedziny f(x)

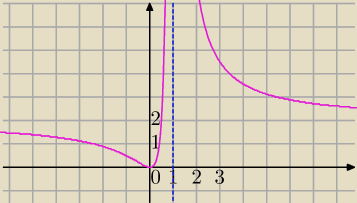
Mila: Wykres

	2x2
f(x)=
	(x−1)2

Poprawka 5) w x=0 ma minimum lokalne. =======================