prostopadłoscian
asdfgh: Podstawą prostopadłościanu jest kwadrat o boku a. Przekątne sąsiednich ścian bocznych,
wychodzących z jednego wierzchołka, tego prostopadłościanu mają dlugośc 10 i tworzą ramiona
kąta o mierze 30.Sporządź odpowiedni rysunek i oblicz:
a)pole przekroju prostopadłościanu płaszczyzną poprowadzoną przez przekątną podstawy i
przeciwległy wierzchołek górnej podstawy
b)oblicz krawędzi tego prostopadłościanu
24 sty 21:27
asdfgh: pomoże ktoś?
24 sty 22:05
Mila:
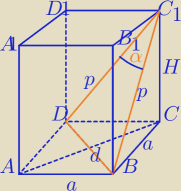
α=30
o
p=10
a) W ΔDBC
1:
| | 1 | | 100 | |
PΔDBC1= |
| *10*10*sin(30o)= |
| =25 |
| | 2 | | 4 | |
P
ΔDBC1=25
b)
|DB|
2=10
2+10
2−2*10*10*cos(30
o)
|DB|
2=200−100
√3=100*(2−
√3)
|DB|
2=2a
2
100*(2−
√3)=2*a
2 /:2
a
2=50*(2−
√3)
a=
√50*
√2−√3=5
√2*
√2−√3=5
√4−2√3=5*
√(1−√3)2=5*|1−
√3|⇔
a=5*(
√3−1)
W ΔBCC
1
p
2=H
2+a
2
10
2=H
2+50*(2−
√3)
100=H
2+100−50
√3
H
2=50
√3
H=
√50*
4√3
H=5
√2*
4√3=5
4√4*
4√3=5
4√12
Odp.
a=5*(
√3−1)
H=5
4√12
=========
24 sty 22:28
asdfgh: Dzięki wielkie
24 sty 22:38
Mila:
24 sty 22:56