Równanie parametryczne prostej Piotrek: Należy napisać równanie parametryczne prostej przechodzącej przez początek układu równań i prostopadłej do płaszczyzny p:(x,y,z)=(1,2,0) + s(−1,0,1) + t(0,1,0) , t,s∊ℛ

utem: P(0,0,0) − punkt przez który przechodzi prosta k. k: x=A*t y=B*t z=C*t, t∊R [A,B,C] wsp. wektora normalnego danej płaszczyzny.

Piotrek: W zadaniu podane jest rónież s więc nie wiem jak do tego mam sie odnieść

Piotrek: Czy ktoś to dokładniej wyjaśni bo nic nie rozumiem z tego

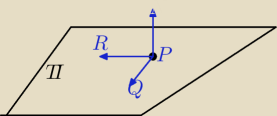
utem: Masz postać parametryczną płaszczyzny; wektory: [−1,0,1], [0,1,0] rozpinają płaszczyznę ( są niewspółliniowe, do niej równoległe). n^→= [−1,0,1] x [0,1,0] wektor prostopadły do płaszczyzny. n^→ będzie wektorem kierunkowym szukanej prostej. http://www.matematyka.pl/142244.htm

utem: n→= [−1,0,1] x [0,1,0] i j k −1 0 1 0 1 0 n^→=[−1,0,−1] Równanie prostej: x=0−1*t y=0+0t z=0−1*t ==========⇔ x=−t y=0 z=−t =========== Nie wiem jak liczyliście na zajęciach, bo można ustalić wektor n^→ za pomocą iloczynu skalarnego.