trygonometria marian: Pytanie do wszystkichoblicz pole trapezu,którego kąty ostre mają miary 45 stopni i 90 stopni, a krótsza podstawa i dłuższe ramie mają długość 6 cm

jaszczur: mają po 6cm czy suma ich jest równa 6

jaszczur: mamy trapez prostokątny niestety nie mogę narysować z cos liczymy dłuższą podstawe cos45=^x−6₆ ^√2₂=^x−6₆ x=3(2+√2) x=6+3√2 z pitagorasa mamy nastepnie wysokość: 6²=(3√2)²+y² y=3√2 teraz pole: P=¹₂(6+6+3√2*3√2 P=18√2+9=9(2√2+1)

marian: maja po 6 cm

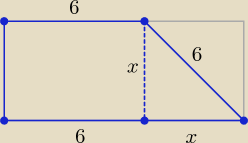Bogdan: W kwestii formalnej − 90^o nie jest miarą kąta ostrego. Bez funkcji trygonometrycznych: 6 = x√2 ⇒ x = 3√2

	1
Pole P =		*(6 + 3√2 + 6)*3√2 = 9(2√2 + 1)
	2

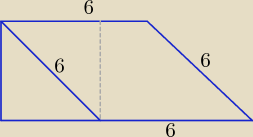Bogdan: albo: pole trapezu jest równe sumie pól: rombu o boku 6 i kącie ostrym 45^o i 1/2 pola kwadratu o przekątnej 6.

	1		62		√2
P = 62sin45o +		*		= 36*		+ 9 = 9(2√2 + 1)
	2		2		2