Wykorzystując monotoniczność oblicz ekstrema Ewelina: f(x) = −x³ +3x +2 x[0,2] Błagam o pomoc i napisanie wskazówek jak robić takie zadania Wiem, że są jakieś tabelki do tego, ale w ogóle tego nie rozumiem

Jerzy: żadne tabelki , tylko liczymy pochodną

Ewelina: w takim razie @Jerzy f' (x)= −3x² +3 co dalej?

Jerzy: kiedy pochodna się zeruje ?

Ewelina: F(0) dla x=−1 lub x=1 przy czym to pierwsze nie należy do dziedziny

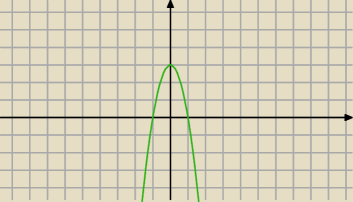
Jerzy: teraz ustal jak pochodna zmienia znak

Ewelina: Nie bardzo rozumiem pytania Skoro interesuje nas dziedzina to rozumiem, że muszę narysować wykres pochodnej funkcji (czyli − 3x² +3) i wywnioskować, że wartość max wynosi 3 dla x=0 i wartość min= 0 dla x=1?

Jerzy: punkt x = −1 nas nie interesuje ( poza dziedziną) jak pochodna zmienia znak w punkcie: x = 1 ( należy do dziedziny) ?

Ewelina: Nie mam pojęcia o co chodzi

Jerzy: zmienia znak z dodatniego na ujemny , a więc tu jest maksimum

Ewelina: więc maximum w tej funkcji =0 dla x=1?

Jerzy: tak

Ewelina: a minimum?

Jerzy: albo f(0) , albo f(2) ... policz

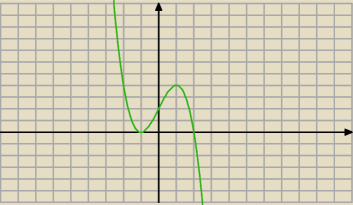
Jerzy: tutaj masz wykres f(x)

Jerzy: oczywiście interesuje nas tylko przedział: [0,2]

Ewelina: min = 4 dla x=1 czyli tak czy inaczej, żeby zobaczyć czy mam dobrze, trzeba narysować ten wykres f?

Jerzy: Max 4 Min 0

Ewelina: okej, dziękuję bardzo