Zbadaj funkcję i narysuj wykres Luku: Mógłby ktoś rozwiązać zadanie z mojego kolokwium? Zbadaj funkcję i narysuj wykres: f(x) = x²*e^x

Jerzy: a co Ty zrobiłe/aś ?

Luku: No dziedzina wiadomo (−∞,∞) i liczyłem granice na krańcach. w −∞ wyszla mi 0 ,a w +∞ wyszla mi +∞. No i przechodząc do asymptot ukośnych , bo poziomych nie ma , natknąłem się na problemy. No , bo schemat rozwiązywania jest dosyć jasny , trzeba sprawdzic w −/+∞ f(x)/x = a i f(x) − ax = b. A w obu tych przypadkach dla + i − wychodzą inne wartości. I nie wiem czy napisać , że nie ma asymptot

Luku: Jak liczę a to wychodzą dwa różne wyniki no i rzecz jasna b też , bo trzeba rozpatrzeć po dwa przypadki dla −/+∞

Jerzy: Dziedzinę i granice masz dobrze, teraz monotoniczność i ekstrema lokalne

Luku: no to liczę , że f'(x) = 2x*e^x + x²*e^x = 0 e^x(x²+2x)=0 /: e^x , bo e^x >0 x(x+2)=0 no to bedzie parabola z miejscami zerowymi −2 i 0 . I teraz mam policzyć ekstrema w tych dwóch punktach czy tylko w zerze , bo tam przechodzi z malejącej w rosnącą ?

Jerzy: w obydwu punktach ma ekstrema lokalne, jakie ?

Luku: A a monotoniczność no to f'(x) > 0 dla x ∊ (−∞,−2) u (0 , ∞) a f'(x)<0 dla x∊(−2,0)

Luku: f(−2) = 4*e⁻2 i f(0) = 0

Jerzy: pytam o ekstrema lokalne

Luku: To trzeba sprawdzić czy pochodna > i < od zera zmienia znak ?

Jerzy: jak pochodna zmienia znak w x = 0 i x = −2

Luku: Nie wiem czy dobrze myślę , ale według tego to z jednego i drugiego podstawienia wychodzi 0

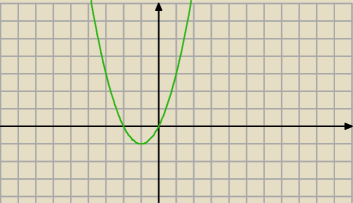
Jerzy: tutaj masz wykres y = x² + 2x ( od tego zależy znak pochodnej) , jak się zmienia ?

Luku: no w (−∞,−2) jest PLUS , w (−2,0) jest MINUS i od (0,+∞) jest PLUS o to chodzi ?

Jerzy: tak , czyli w punkcie: x = −2 jest maksimum,a w : x = 0 minimum asymptota pozioma: y = 0 już masz wszystko, możesz rysować wykres

Luku: A po czym pan wywnioskował , że istnieje asymptota pozioma ? Tego nie mogę zrozumieć

Jerzy: lim_x→−∞ = 0

Luku: Ahaaaa. Bardzo bardzo dziękuję za pomoc i cierpliwość . Pozdrawiam

Jerzy: Powodzenia