położenie dwóch okręgów
gemmai: 3.152
Dla jakich wartości m (m∊R) okręgi opisane równaniami:
o1: (x−m)2 + (y+1)2 = 8 oraz o2: (x+1)2 + (y−m)2 = 2 są zewnętrznie styczne? Dla
znalezionych wartości parametrów wykonaj ryzunek. Oblicz współrzędne punktu styczności A.
23 sty 19:43
Janek191:
S
1 =( m, − 1) S
2 = ( − 1, m)
r
1 = 2
√2 r
2 =
√2
Obliczam odległość I S
1S
2 I
I S
1 S
2 I =
√( − 1 − m)2 + ( m +1)2 =
√ 1 + 2m + m2 + m2 + 2m + 1 =
√2 m2 + 4m +2
Musi być
I S
1 S
2 I = r
1 + r
2
czyli
√2 m2 + 4m + 2 =2
√2 +
√2 = 3
√2
2 m
2 + 4m + 2 = 9*2 = 18
2 m
2 + 4 m − 16 = 0 / : 2
m
2 + 2m − 8 = 0
Δ = 4 − 4*1*(−8) = 4 + 32 = 36
√Δ = 6
| | − 2 − 6 | | − 2 + 6 | |
m = |
| = − 4 lub m = |
| = 2 |
| | 2 | | 2 | |
======================================
23 sty 19:50
Janek191:
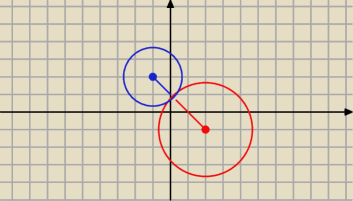
m = 2
( x − 2)
2 + ( y + 1)
2 = 8 ( x + 1)
2 + ( y − 2)
2 = 2
A = ( 0, 1) − punkt styczności
23 sty 19:55