 x2 + y2 + 6 x + 2 y + 5 = 0
( x + 3)2 − 9 + ( y + 1)2 − 1 + 5 = 0
( x + 3)2 + ( y + 1)2 = 5
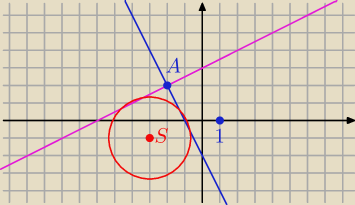
S = ( − 3, − 1) r = √5
A = ( − 2, 2)
y = a x + b przechodzi przez A ,więc
2 = − 2a + b ⇒ b = 2 a + 2
y = a x + 2 a + 2
lub
a x − y + 2a + 2 = 0
Odległość tej prostej od S jest równa √5
x2 + y2 + 6 x + 2 y + 5 = 0
( x + 3)2 − 9 + ( y + 1)2 − 1 + 5 = 0
( x + 3)2 + ( y + 1)2 = 5
S = ( − 3, − 1) r = √5
A = ( − 2, 2)
y = a x + b przechodzi przez A ,więc
2 = − 2a + b ⇒ b = 2 a + 2
y = a x + 2 a + 2
lub
a x − y + 2a + 2 = 0
Odległość tej prostej od S jest równa √5
| I − 3 a − 1*(−1) + 2 a + 2 I | |
= √5 | |
| √a2 + 1 |
| − 3 − 5 | − 3 + 5 | |||
a = | = − 2 lub a = | = 0,5 | ||
| 4 | 4 |