Potęgowanie - zespolone motzny: 2 ¹20 (−cos ³₄ 120pi + sin ³₄ 120pi) Pierwotnie wygląda to tak : (−√2 + √2i)¹20 Ps/ To jest 2 do potęgi 120, tylko dziwnie tutaj na forum wygląd zmienia. Jak to rozbić, w wyniku ma wyjść 1.

Janek191: ( −√2 + √2 i)¹²⁰ = (( −√2 + √2 i)²}⁶⁰ = (2 − 4 i − 2)⁶⁰ = = ( − 4 i)⁶⁰ = (−4)⁶⁰*(i⁶⁰) = 2¹²⁰*( −1)³⁰ = 2¹²⁰*1 = 2¹²⁰

motzny: Up@, a dlaczego pominąłeś cos i sin?

Janek191: Nie korzystałem z postaci trygonometrycznej

Mila: Tam jest:

	3		3
2120*[−cos(		*120π)+i sin(		*120π)] =
	4		4

? Może zapisz zadanie "od początku":

motzny: (−√2 + √2i)¹20 <−−− cały nawias do potęgi 120

Mila: To zrób tak, jak Janek. Postać trygonometryczną masz błędną.

	3π		3π
z120=2120*(cos(		*120)+i sin(		*120) )=
	4		4

=2¹²⁰*(cos(90π)+i sin (90π) )= =2¹²⁰*(cos(45*2π)+i sin (45*2π) )= =2¹²⁰*(1+0)=2¹²⁰

motzny: A czy Ty Mila, rozbiłaś trygonometryczną na 2, że wyszło Ci cos i sin po 45 czy jak? Bo nie rozumiem zasady działania tego momentu w 2 linijce od dołu.

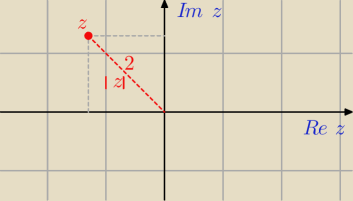
Janek191: z = − √2 + √2 i więc I z I = √( −√2)² + (√2])² = 2

	− √2		√2
cos φ =		sin φ =
	2		2

więc

	π		π		3
φ = 90o + 45o =		+		=		π
	2		4		4

	3		3
z = 2*( cos		π + i sin		π)
	4		4

oraz

	3		3
z120 = 2120*( cos (		π*120 )+ i sin (		π* 120 ) ) =
	4		4

= 2¹²⁰*( cos 90π + i sin 90π ) = 2¹²⁰*( cos 45*2π + i sin 45*2π) = = 2¹²⁰*( cos 2π + i sin 2π) = 2¹²⁰*( cos 0 + i sin 0 ) = = 2¹²⁰*( 1 + i *0) = 2¹²⁰