stereometria Madzia: Sześcian,którego krawędź ma długość a,rozcięto na dwie części płaszczyzną przechodzącą przez jedną z krawędzi i nachyloną pod kątem 30' do płaszczyzny ściany zawierającej tę krawędź. Oblicz pole powierzchni całkowitej i objętość każdej części.

bonawentura: jakby spojrzeć na sprawę 2 płaszczyznowo i wziąć pod uwagę jeden bok, ten z którego widać, że płaszczyzna przechodzi pod kątem 30', mamy kwadrat z wydzielonym trójkątem prostokątnym o kątach 30, 90... ostatni musi mieć 60, więc z właściwości takiego trójkąta wiemy, żę skoro dłuższa przyprostokątna ma a, to krótsza ma a/2, obliczamy pole tego trójkąta i mnożymy przez a, otrzymujemy pole tej części, pole drugiej części można obliczyć odejmując po prostu pole pierwszej części od pola całkowitego, czyli a³ − (1/4 a *a)*a możemy też obliczyć pole trapezu w podstawie i pomnożyć przez a. jedna podstawa trapezu ma a, a druga a−a/2, czyli... a/2 (dobrze widać na rysunku), wysokość to także a, czyli pole trapezu to 1/2 (a/2+ a) *a mnożąc to przez a otrzymujemy pole 2 części pola powierzchni pole pierwszej części(z trójkątami w podstawach ) = 2* (1/4a*a) + a*a + a/2 * a pole 2 części = 2* 1/2 (a/2+a)*a + 2*a*a + a/2 *a

bonawentura: stop, pokręciłem....

bonawentura: wszędzie zamiast a/2 będzie a/√3

bonawentura: na rysunku to widać...

bonawentura: jeszcze raz pole pow I = 1/2* a/ √3 *a *a pole pow 2 = 1/2* (a/√3 + a) *a * a obwób 1 = 2* 1/2 a/√3 *a + a*a + 2 a/√3 *a + a/ √3 *a obwód 2 = 2* 1/2 (a/√3 +a)*a + 2a*a + 2 a/√3 *a + a/√3 *a

bonawentura: coś takiego chyba ale może być jakiś błąd... może cię jakoś chociaż nakieruję

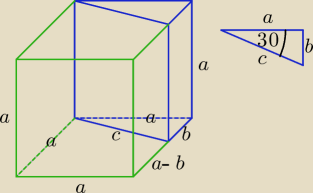
Bogdan: b = a*tg30^o

	a
c =
	cos30o

Madzia: dzięki wielkie