 h=2r= 8
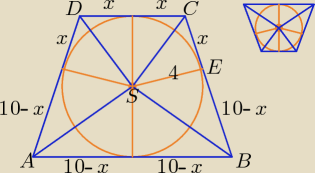
oznaczając IRCI=IDRI=ICKI=IDLI= x
to IKBI=IBNI=ANI=ALI= 10 −x , dla x €(0,10)
Jedna część obwodu to: 4*x
druga cz. obwodu to 4*(10−x)
to szukany stosunek tych częśći obwodu:
h=2r= 8
oznaczając IRCI=IDRI=ICKI=IDLI= x
to IKBI=IBNI=ANI=ALI= 10 −x , dla x €(0,10)
Jedna część obwodu to: 4*x
druga cz. obwodu to 4*(10−x)
to szukany stosunek tych częśći obwodu:
| 4(10 −x) | (10−x) | |||
k= | = | |||
| 4x | x |
| 10−2 | ||
k= | = 4
| |
| 2 |
 Dobry wieczór.
Można również skorzystać z podobieństwa trójkątów: BSE i CSE otrzymując proporcję
(nie przyjmuję założenia, że dolna podstawa jest dłuższa od górnej):
Dobry wieczór.
Można również skorzystać z podobieństwa trójkątów: BSE i CSE otrzymując proporcję
(nie przyjmuję założenia, że dolna podstawa jest dłuższa od górnej):
| x | 4 | ||
= | ⇒ x2 − 10x + 16 = 0 ⇒ x = 2 lub x = 8 | ||
| 4 | 10 − x |
| 4x | 4 (10 − x) | |||
Obliczamy stosunek: k = | lub k = | |||
| 4 (10 − x) | 4x |
| 4*2 | 1 | 4*8 | ||||
Dla x = 2: k = | = | lub k = | = 4 | |||
| 4*8 | 4 | 4*2 |
| 4*8 | 4*2 | 1 | ||||
dla x = 8: k = | = 4 lub k = | = | ||||
| 4*2 | 4*8 | 4 |
