Warunek prostopadłości prostych, wyznaczanie trzecego wierzchołka trójkąta Kinga: W trójkącie ABC znane są wierzchołki A(0,0) oraz B(4,−1). Wiadomo, że w punkcie H(3,2) przecinają się proste zawierające wysokości tego trójkąta. Wyznaczyć współrzędne wierzchołka C. Sporządzić rysunek. Proszę o pomoc

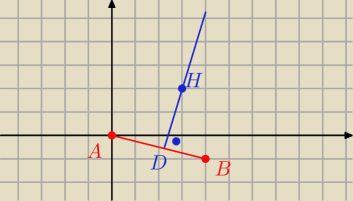
Janek191: Wyznacz prostą DH.

Kinga: wyznaczyłam prostą DH, jej równanie wyszło mi y=4x − 10

Kinga: ale nie wiem czy to dobrze, słabo to rozumiem

Janek191: Następnie wyznacz proste: BH i AC prostopadłą do BH AH i BC prostopadłą do AH Proste AC i BC przetną się w punkcie C.

Janek191: Dobrze : )

Kinga: czyli nie ma jakiegoś wzoru do tego? bo mi nauczyciel mówił, ze trzeba tutaj wykorzystać te wzory na prostopadłość prostych i dlatego narysowałam tą prostą i obliczyłam jej równianie.Czyli zrobiłam to niepotrzebnie?

Kinga: a nie, już chyba rozumiem

Kinga: cóż, wyszło mi trochę dziwnie, wg moich obliczeń punkt C ma współrzędne : x − 33/10 y − 11/10

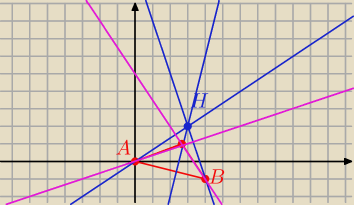
Janek191: Prosta BH B =( 4, −1) H = (3,2)

	2 −(−1)
a1 =		= − 3
	3 −4

y = − 3x + b₁ 2 = −3*3 + b₁ ⇒ b₁ = 11 y = − 3 x + 11 ========= A = (0, 0) Prosta AC

	1
y =		x + b2
	3

0 = 0 + b₂ ⇒ b₂ = 0

	1
y =		x
	3

========= Prosta AH A =(0, 0) H = (3,2)

	2
a3 =
	3

	2
y =		x + b3
	3

	2
2 =		*3 + b3 ⇒ b3 = 0
	3

	2
y =		x
	3

=========== Prosta BC y = −1,5 x + b₄ B = ( 4, −1) − 1 = − 6 +b₄ ⇒ b₄ = 5 y = − 1,5 x + 5 ============

1
	x = − 1,5 x + 5 / *3
3

x = − 4,5 x + 15 5,5 x = 15

	15		150		30
x =		=		=
	5,5		55		11

	1		30		10
y =		*		=
	3		11		11

	30		10
C = (		,		)
	11		11

====================

Janek191: ?

Kinga: dziękuję, już wiem gdzie popełniłam błąd źle obliczyłam równanie AC