Okrąg wpisany Descr: Wyznacz równanie okręgu wpisanego w trójkąt równoramienny o wierzchołkach A=(2,−2), B=(8,4) oraz C=(−4,10).

	54
Proszę o pomoc, wyznaczyłem jedynie promień okręgu r=		, ale nie mam pojęcia co
	3√2+6√5

dalej.

Eta:

	54
r=		= 2√5−√2
	3√2+6√5

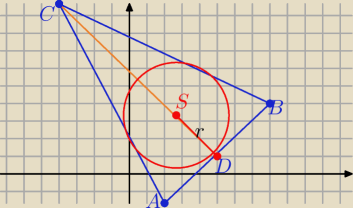
Środek S tego okręgu znajduje się w punkcie przecięcia dwusiecznych kątów trójkąta to S∊ prostej DC ( która jest jednocześnie dwusieczną 1/ wyznacz równanie prostej DC ................ y= −x+6 2/ S( x, −x+6) Odległość S od prostej AB d=r AB: y= x−4 stąd wyznaczysz S(x, y) o: ( x−x_S)²+(y−y_S)²= r² i licz.......... rachunki "paskudne" ( może dostałeś to zadanie za karę

Descr: Obliczyłem już trochę innym sposobem − wyliczyłem prostą zawierającą się w dwusiecznej kąta CAB, dalej punkt przecięcia z prostą CD i otrzymałem wynik. Fakt, rachunki paskudne, wynik też, ale zadanie celowo wybrałem takie "ambitniejsze"

Eta:

Mila: DC^→=[−9,9] DS^→=[−9k,9k] , k>0, zgodne zwroty |DS|=√81k²+81k² √161k²=2√5−√2 9√2k=2√5−√2 /*√2 9*2*k=2√10−2

	√10−1
k=
	9

DS^→=[1−√10,√10−1] D=(5,1)→T_DS^→⇒S=(6−√10, √10) ==========================

Eta: Jeszcze .... r= ?

Mila: r wyznaczyłaś.