co zrobilem zle
pies: √x2−9>√2x+3√2
Df:x2−9≥0⇒x∊R
√2x+3√2≥0 ⇒x∊<−3,+00)
a w odp mam (−oo,−1) co kluci sie z moja dizedzina
21 sty 16:02
Metis: Źle rozwiązujesz.
x2−9≥0
21 sty 16:13
pies: i co dalej ? wychodzi mi ze
√x2−9>√2x+3√2
x2=−11
21 sty 16:15
Metis: Masz złą dziedzine.
21 sty 16:26
olekturbo: Dziedzina to nie tylko x2−9 ≥ 0, a również √2x+3√2 ≥ 0
21 sty 16:28
pies: no chyba nie bardzo ....bo wychodzi x≥−3 a w odp mam −oo,0
21 sty 18:07
pies: zrobi ktos to zad cale prosze
21 sty 18:11
Metis: Poczytaj zadania rozwiązane w podręczniku.
21 sty 18:16
pies: nie mam podrecznika ..ale przeciez √2x+3√2 ≥ 0 to nie moze tak byc bo w zad nie jest = tylko >
21 sty 18:17
Kacper:
D=(−∞,−3>∪<3,+∞)
21 sty 18:18
pies: nie rozumiem skad to wzioles?
ja podzielilem pr zez v2 i mi wyyszlo x+3≥0 ⇒x≥−3
21 sty 18:22
Metis: Liczba podpierwiastkowa większa od 0.......
21 sty 18:23
pies: tez sie nie zgadza ostateczna odp to −oo,−1 wiec masz zle
21 sty 18:24
Kacper:
Dziedzina, a rozwiązanie to nie to samo.
21 sty 18:26
pies: to powiedz jak to zrobic zrobisz to ? bo na razie to masz zle
21 sty 18:30
Kacper:
Nie będę udzielał odpowiedzi, bo oczywiście mam dobrze, tylko ty nie rozumiesz co ja napisałem.
21 sty 18:33
Metis: Napisałem Ci na początku, że masz złą dziedzinę i podałem co źle liczysz

21 sty 18:35
Mila:
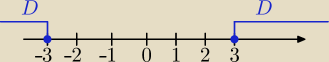 √x2−9
√x2−9>
√2x+3
√2
√x2−9≥0 dla x≤−3 lub x≥3
Zatem z prawej strony może być liczba ujemna ≤−3, bo każda dodatnia jest od niej większa.
1) x≥3
√x2−9>
√2x+3
√2⇔
√(x−3)*(x+3)>
√2(x+3) /
2
(x−3)*(x+3)>2*(x+3)
2
(x−3)*(x+3)−2*(x+3)
2>0
(x+3)*[x−3−2(x+3)]>0
(x+3)*(x−3−2x−6)>0
(x+3)*(−x−9)>0
x=−3, x=−9
x∊(−9,−3) ∉<3,
∞) brak rozwiązania w tym przedziale.
b) x≤−3 wtedy
L=
√x2−9≥0
Sprawdzamy prawą stronę.
x≤−3
x=−3
L=
√9−9=0
P=
√2*(−3+3)=0 nierówność nie jest spełniona dla x=−3
x<−3 /+3
x+3<0 /*
√2
√2*(x+3)<0 zatem
√x2−9>
√2(x+3) dla każdej liczby x<−3
=============================
Odp. x<−3
21 sty 18:42
kyrtap: Pani
Mila pięknie rozwiązania daje

21 sty 18:44
kyrtap: piękne *
21 sty 18:45
pies: dziekuje mila jest bardzo mila

21 sty 18:45
pies: ale odp do tego zadania to (−oo,−1) wiec masz zle
21 sty 18:46
Mila:
To odp. jest nieprawidłowa.
√(−2)2−9=√4−9=√−5 nie istnieje.
Sprawdź, czy dobrze przepisałeś nierówność.
21 sty 18:49
pies: tak i sprawdzlaem 10 razy ...odp x∊(−oo,−1)
a tego warunku nie ma tak ?√2x+3√2 ≥ 0
21 sty 18:50
pies: dlaczego nie m oge podzielic przez √2 tutaj √x2−9>√2x+3√2
21 sty 18:55
Mila:
x≥3 to √2(x+3)>0 i masz obie strony nierówności nieujemne, podnosimy do kwadratu (1) punkt.
21 sty 18:55
pies: ale dlaczego nie m oge podzielic przez √2 tutaj √x2−9>√2x+3√2
21 sty 18:57
21 sty 18:57
pies: √x
2−9>√2x+3√2 //v2
√x2−9 /
√2>x+3 //
2
x
2−9 /2>x
2+9
x
2−9−18>x
2
0=... zrobilem blad

21 sty 19:06
pies: a tego warunku nie ma ?√2x+3√2 ≥ 0 a moze byrc taki wogole warunek

? bo w tresci zad jest > a
nie = −−−>√x2−9>√2x+3√2
21 sty 19:09
Mila:
Zrobiłeś , bo nie umiesz stosować wzorów skróconego mnożenia.
Warunek jest potrzebny, jeżeli chcesz podnosić obie strony nierówności do kwadratu, możesz to
zrobić,
gdy obie strony są nieujemne.
(x+3)
2=x
2+6x+9
x
2−9>2x
2+12x+18
x
2+12x+27<0
po rozwiązaniu:
x∊(−9,−3)
Przeczytaj uważnie moje rozwiązanie i postaraj się zrozumieć.
21 sty 19:23
Metis: (x+3)2...
Trzeba nauczyć się podstaw. Bo my tlumaczymy, a ty nic z tego nie rozumiesz.
21 sty 19:23
pies: a tak nie zauwazylem ..... "zrobić,
gdy obie strony są nieujemne."

?jak to really nikt tak nie robi matemaks tak nie robi...ale
pytalem czy taki warunek sie robi √2x+3√2 ≥ 0

bo z tego wynika ze x≥−3
21 sty 19:33
Mila:
Tak, ale musisz jeszcze uwzględnić dziedzinę wyrażenia √x2−9,
co masz uwzględnione w pkt(1).
x≥−3 i x≥3⇔x≥3
21 sty 19:39
21 sty 19:41
pies: czekaj
Df:
2x+3√2 ≥ 0 ⇒x≥−3
√x2−9≥0 ⇒x∊(−oo,−3)U(3,+oo)
i teraz czesc wpolna to ... nie powinna byc

x∊(3,+oo)jestem glupi
21 sty 19:44
Metis: Dziedzina to nie to samo co założenia płynące ze sposobu rozwiązywania zadania.
21 sty 19:45
pies: ale w innych zad z tego ttpu np √3x+1=x+1
dziedzina bylo 3x+1≥0 i x+1≥0 wiec
21 sty 19:46
Metis: Dziedzina : 3x+1≥0 .
Wdrążam, stosuje pewny sposób rozwiązania−rozumowania, który wymaga dodatkowych założeń.
Dlatego x+1≥0
Wtedy obie strony nierównosci są nieujemne.
Nie chce Ci mącić w głowie.
21 sty 19:49
ZKS:
Dziedzina tego równania to tylko i wyłącznie 3x + 1 ≥ 0.
21 sty 19:49
pies: no dobrze dziekuje tloczki za pomoc:(
21 sty 19:57

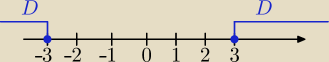 √x2−9>√2x+3√2
√x2−9≥0 dla x≤−3 lub x≥3
Zatem z prawej strony może być liczba ujemna ≤−3, bo każda dodatnia jest od niej większa.
1) x≥3
√x2−9>√2x+3√2⇔
√(x−3)*(x+3)>√2(x+3) /2
(x−3)*(x+3)>2*(x+3)2
(x−3)*(x+3)−2*(x+3)2>0
(x+3)*[x−3−2(x+3)]>0
(x+3)*(x−3−2x−6)>0
(x+3)*(−x−9)>0
x=−3, x=−9
x∊(−9,−3) ∉<3,∞) brak rozwiązania w tym przedziale.
b) x≤−3 wtedy
L=√x2−9≥0
Sprawdzamy prawą stronę.
x≤−3
x=−3
L=√9−9=0
P=√2*(−3+3)=0 nierówność nie jest spełniona dla x=−3
x<−3 /+3
x+3<0 /*√2
√2*(x+3)<0 zatem
√x2−9>√2(x+3) dla każdej liczby x<−3
=============================
Odp. x<−3
√x2−9>√2x+3√2
√x2−9≥0 dla x≤−3 lub x≥3
Zatem z prawej strony może być liczba ujemna ≤−3, bo każda dodatnia jest od niej większa.
1) x≥3
√x2−9>√2x+3√2⇔
√(x−3)*(x+3)>√2(x+3) /2
(x−3)*(x+3)>2*(x+3)2
(x−3)*(x+3)−2*(x+3)2>0
(x+3)*[x−3−2(x+3)]>0
(x+3)*(x−3−2x−6)>0
(x+3)*(−x−9)>0
x=−3, x=−9
x∊(−9,−3) ∉<3,∞) brak rozwiązania w tym przedziale.
b) x≤−3 wtedy
L=√x2−9≥0
Sprawdzamy prawą stronę.
x≤−3
x=−3
L=√9−9=0
P=√2*(−3+3)=0 nierówność nie jest spełniona dla x=−3
x<−3 /+3
x+3<0 /*√2
√2*(x+3)<0 zatem
√x2−9>√2(x+3) dla każdej liczby x<−3
=============================
Odp. x<−3



 ? bo w tresci zad jest > a
nie = −−−>√x2−9>√2x+3√2
? bo w tresci zad jest > a
nie = −−−>√x2−9>√2x+3√2
 ?jak to really nikt tak nie robi matemaks tak nie robi...ale
pytalem czy taki warunek sie robi √2x+3√2 ≥ 0
?jak to really nikt tak nie robi matemaks tak nie robi...ale
pytalem czy taki warunek sie robi √2x+3√2 ≥ 0  bo z tego wynika ze x≥−3
bo z tego wynika ze x≥−3










 x∊(3,+oo)jestem glupi
x∊(3,+oo)jestem glupi