Zastosowanie pochodnej funkcji Liceum/Technikum Paulina: Wyznacz najmniejszą i największą wartość funkcji f danej wzorem.

	3−x2
f(x)=		w przedziale <−1;3>
	x2 + 1

Staszek:

	−2x*(x2+1)−2x*(3−x2)		−2x3−2x−6x+2x3		−8x
f'(x)=		=		=
	(x2+1)2		(x2+1)2		(x2+1)2

mianownik dodatni dla każdego x, więc funkcja rośnie <−∞,0> i maleje <0,+∞> z tego wynika największa wartość dla x=−1, a najmniejsza dla x=3

	6
odpowiednio równe 2 i −
	10

Janek191:

	− 2 x*(x2 + 1) − ( 3 − x2)*2x
f '(x) =		=
	(x2 + 1)2

	− 2x3 −2 x − 6 x + 2x3		− 8 x
=		=
	(x2+1)2		(x2 + 1)2

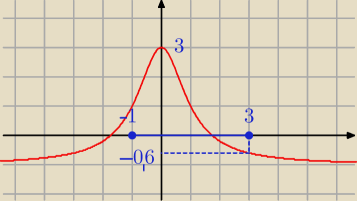
Mianownik jest zawsze > 0, więc f '(x) < 0 dla x > 0 oraz f '(x) > 0 dla x < 0 zatem w ( − ∞, 0) funkcja rośnie , a w ( 0, + ∞) funkcja maleje. y_max = f(0) = 3

	− 6
ymin = f( 3) =
	10

Patrz też na wykres

piotr1973:

	−8 x
f`(x) =
	(x2+1)2

f`(0)=0 czyli liczysz f(−1)=1 f(0)=3 f(3)=−3/5 i wybierasz max i min