analiza matematyczna
Paulina: dana jest funkcja f(x)=x3+4x2 −3x −12 x∊R
napisz rownanie stycznej do wykresu funkcji f w punkcie A w ktorym wykres funkcji f przecina os
OY
20 sty 20:48
Qulka: y=−3x−12
20 sty 20:51
Paulina: −12 rozumiem , ale skad y=−3x

a=f'x

20 sty 20:53
Qulka: a=f'(x0) a w tym wypadku x0=0
20 sty 20:54
Paulina: a=f'(x)
dlaczego wybrac 1

20 sty 20:56
Jack: ?
skad 2przypadki?
f ' (x) = 3x2 + 8x − 3
f ' (0) = −3
20 sty 20:57
Janek191:
Funkcja przecina oś OY dla xo = 0.
20 sty 20:58
Paulina: jeszcze b)
Punkt B nalezy do wykresu funkcji f.styczna do wykresu w tym punkcie jest rownolegla do
stycznej w punkcie A.Wyznacz wspolrzedne punktu B oraz rownanie stycznej do wykresu funkcji f
w tym punkcie
20 sty 20:59
Paulina: dziekuje za wytlumaczenie
20 sty 21:00
Janek191:
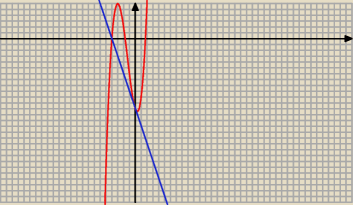
20 sty 21:01
Paulina: zalapalam o co chodzi. a drugi podpunkt

Punkt B nalezy do wykresu funkcji f.styczna do wykresu w tym punkcie jest rownolegla do
stycznej w punkcie A.Wyznacz wspolrzedne punktu B oraz rownanie stycznej do wykresu funkcji f
w tym punkcie
20 sty 21:03
Qulka: f'(x)=−3 rozwiązujesz x=0 to A oraz x=−8/3 to B
podstawiasz f(−8/3) i wyliczasz y B
20 sty 21:07
Janek191:
y = − 3 x + b
− 3 x + b = x3 + 4 x2 − 3 x − 12
20 sty 21:08
Paulina: b=x3+4x2−12
20 sty 21:13
Paulina: nie rozumiem i co dalej mam zrobic?
20 sty 21:15
Paulina: moze to ktos rozjasnic

20 sty 21:28
Qulka: a zrób to co ja napisałam
20 sty 21:29
 a=f'x
a=f'x


 Punkt B nalezy do wykresu funkcji f.styczna do wykresu w tym punkcie jest rownolegla do
stycznej w punkcie A.Wyznacz wspolrzedne punktu B oraz rownanie stycznej do wykresu funkcji f
w tym punkcie
Punkt B nalezy do wykresu funkcji f.styczna do wykresu w tym punkcie jest rownolegla do
stycznej w punkcie A.Wyznacz wspolrzedne punktu B oraz rownanie stycznej do wykresu funkcji f
w tym punkcie
