dgdgd
Nati: Poziom hard
Wysokosc ostroslupa prawidlowego szesciokatnego rowna sie 12. Stosunek pola jednej sciany
bocznej ostroslupa do pola jego podstawy rowna sie 1:3. Oblicz Pc i V
20 sty 20:08
piotr: prościzna
20 sty 20:21
Nati: mozna prosic o pomoc?
20 sty 20:24
GIGANT: Hmmm z tego stosunku pole jednej ściany bocznej wynosi Pb =
12 * a * h , pole podstawy to
sześć trójkątów równobocznych czyli Pp = 6 * a
2√3 / 4
| | Pb | | 1 | |
Teraz równość : |
| = |
| będą dwie niewiadome a oraz h. h to oczywiście wysokość |
| | Pp | | 3 | |
ściany bocznej, gdybyśmy znali np długość trójkata w podstawie to wtedy z pitagorasa można by
było ładnie podstawić. Może coś mi wpadnie do głowy
20 sty 20:27
GIGANT: no przecież ! wysokośc w trójkącie równobocznym wyraża się wzorem h = a√3 / 2
20 sty 20:29
GIGANT: Nati wiesz o co mi chodzi? Mamy trójkąt prostokątny. Jeden bok to wysokość tego ostrosłupa (
pada pod kątem prostym ), drugi bok to wysokość trójkąta w podstawie, a trzeci bok (
przeciwprostokątna ) to wysokośc ściany bocznej.
20 sty 20:31
GIGANT: Nie liczę tego ale widzę, że sie da policzyć.
Będzie 12
2 + (a
√3/2)
2 = h
2 sa dwie niewiadome a i h więc potrzebne jeszcze jedno równanie
( korzystając z tego stosunku ) jest podane wyżej. Daj znać jak wyszło, jav wrócę to też
policze

20 sty 20:40
Nati: niestety mi za skarby swiata nie chce to wyjsc, wychodza liczby z kosmosu..
20 sty 21:24
Mila:
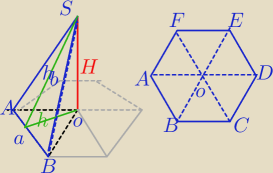
H=12
| | 6*a2√3 | | 3a2√3 | |
P6−kata= |
| = |
| |
| | 4 | | 2 | |
h
b=a
√3
h
b2+h
2=H
2
============
| | 8√15 | | 8*√45 | | 8*3*√5 | |
hb= |
| *√3= |
| = |
| |
| | 5 | | 5 | | 5 | |
| | 1 | | 8√15 | | 24√5 | |
Pb=6* |
| * |
| * |
| |
| | 2 | | 5 | | 5 | |
| | √75 | | √25*3 | |
Pb=576* |
| =576* |
| |
| | 5 | | 5 | |
P
b=576
√3
============
Dalej licz sama.
20 sty 23:25

 H=12
H=12