proszę o pomoc cinek: Boki trójkąta mają długości |AB|=8, |BC|=7, |AC|=12. Oblicz długości odcinków, na które każda z dwusiecznych dzieli przeciwległy bok.

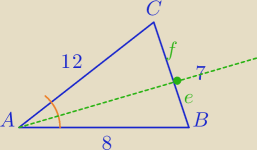
Mila: Dwusieczna kąta A; Z tw. o dwusiecznej:

8		12
	=		⇔8f=12e /:4⇔2f=3e
e		f

e+f=7⇔e=7−f −−−−−−−−−−− 2f=3*(7−f) 2f=21−3f 5f=21

	21
f=		=415
	5

e=7−4¹₅=2⁴₅ ================ Tak postępujesz z każdą dwusieczną.

cinek: dziękuje. trudne to(:

Mila: Nie jest trudne. Popatrz na rysunek i zrozumiesz.

cinek: ale jak z każdą dwusieczną ? to to nie koniec?

Mila: Masz trzy kąty, to trzy dwusieczne. Teraz narysuj jeszcze raz ΔABC i dwusieczną kąta B. Potem dwusieczną kąta C.

Wiem: Po prostu widzisz: Dla boku |AB|=8 istnieją ewidentne zależności:

8

7

12

8−x

a1

x

a1

=

=

⋀

=

⋀

=

sinα

sinβ

sinγ

sin0,5α

sinβ

sin0,5α

sinγ

	1		18
A rozwiązaniem takiego układu są długości 5		i 2
	19		19

Pozostałe boki analogicznie,po krótkich obliczeniach sama dojdziesz

cinek: dziękuje już ogarniam

Mila: https://matematykaszkolna.pl/strona/498.html

Odblokowany obywatel: A na forum i po za nim(i to też) nadal bezczelne jeszcze publicznie nie wyjebane w odbytnicę policyjne małpy,technicznie uprzywile jo w ani dygnitarze