Równanie kwadratowe z parametrem Vuko: Wyznacz wszystkie wartości parametru m, dla których suma kwadratów rozwiązań równania x²−(m−3)x+m=0 pomniejszona o 9 osiąga najmiejszą wartość. Ile ta wartość wynosi?

Jerzy: 1) Δ > 0 2) g(x) = x₁² + x₂² − 9 = (x₁ + x₂)² − 2x₁*x₂ .. i szukamy minimum

Vuko: Dzięki Jerzy

Vuko: Ale jak szukamy minimum? Nie mam określonego przedziału, w którym minimum musi się zawierać.

Jerzy: ad 2) Jaką masz funkcję g(m) ?

Jerzy: szykasz tylko tam, gdzie spełniony jest pierwszy warunek

Vuko: wychodzi mi coś takiego: Δ>0 <=> xe(−∞,1) i (9,+∞) gdzie mam tutaj szukać wartości najmniejszej dla g(m) skoro przedziały nie są domknięte?

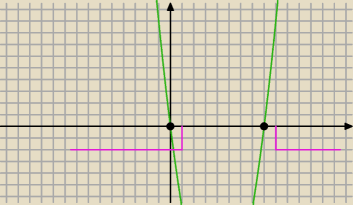
Jerzy: g(m) = m² − 8m szukasz minimum w przedziale (0,1) ... patrz wykres

Jerzy: masz rację , rzeczywiście nie ma jak znaleźć minimum jedynie co można zrobić, to przyjąć: Δ ≥ 0 ( nie ma mowy o różnych pierwiastkach ) i wtedy g_min = g(1)

Vuko: ja też tak myślałem, w odpowiedziach jest napisane że jest to g(4)=16

Jerzy: no to jest katastrofa w odowiedziach, bo co prawda g(4) = − 16 to minimum, ale m = 4 nie spełnia 1 warunku, czyli nie ma dwóch pierwiastków

Janek191: Δ = ( m −3)² − 4*1*m = m² − 6 m + 9 − 4 m = m² − 10 m + 9 m² − 10 m + 9 > 0 Δ_m = 100 − 4*1*9 = 64 p{Δ_m) = 8

	10 − 8
m1 =		= 1 m2 = 9
	2

m ∊ ( − ∞; 1) ∪ ( 9 , +∞ ) x₁² + x₂² − 9 = ( x₁ + x₂)² − 2 x₁*x₂ − 9 = (m −3)² − 2*m − 9 = m² − 6m + 9 − 2m − 9 f(m) = m² − 8 m = m*( m − 8)

	8
p =		= 4 ∉ D
	2