 (1)
z=x+iy, x,y∊R
|z−2i|=im(z)
|x+iy−2i|=y, y≥0
√x2+(y−2)2=y /2
x2+y2−4y+4=y2
x2−4y+4=0
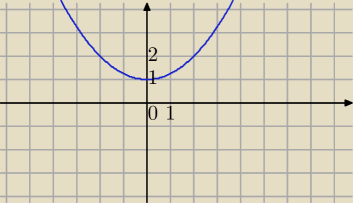
4y=x2+4
(1)
z=x+iy, x,y∊R
|z−2i|=im(z)
|x+iy−2i|=y, y≥0
√x2+(y−2)2=y /2
x2+y2−4y+4=y2
x2−4y+4=0
4y=x2+4
| 1 | ||
y= | x2+1 | |
| 4 |
 2)
| z + i | = | z − 2 |⇔
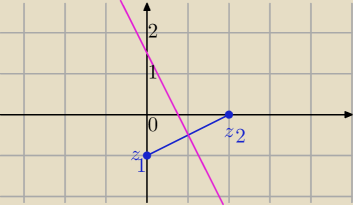
Interpretacja geometryczna
|z−(−i)|=|z−2| to symetralna odcinka o końcach (0,−1) i (2,0)
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
Możesz zrobić tak jak w pierwszym zadaniu
z=x+iy
√x2+(y+1)2=p{
2)
| z + i | = | z − 2 |⇔
Interpretacja geometryczna
|z−(−i)|=|z−2| to symetralna odcinka o końcach (0,−1) i (2,0)
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
Możesz zrobić tak jak w pierwszym zadaniu
z=x+iy
√x2+(y+1)2=p{ x−2)2+y2
Stąd
x−2)2+y2
Stąd
| 3 | ||
y=−2x+ | ||
| 2 |