Oblicz ekstremum lokalne funkcji Nitta: ekstremum lokalne f(x)=2/x=x/2 Umie ktoś to zrobić

Nitta: f(x)=2/x+x/2 Umie ktoś to zrobić

Qulka: policz pochodną

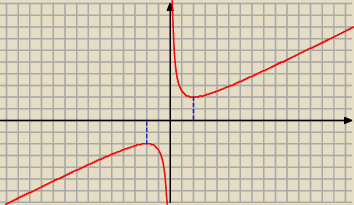
Janek191: Wiele osób to umie D = ℛ \ { 0 }

	2		x
f(x) =		+
	x		2

	−1		2
f '(x) = 2*		+ 0,5 = −		+ 0,5 = 0 ⇔ x2 = 4 ⇔ x = − 2 lub x = 2
	x2		x2

Dla x < − 2 jest f '(x) > 0 , a dla x > − 2 jest f '(x) < 0 czyli mamy maksimum lokalne w x = − 2 Dla x < 2 jest f'(x) < 0, a dla x > 2 jest f '(x) > 0 czyli mamy minimum lokalne dla x = 2.

PW: Nawet w liceum jest stosowane twierdzenie dla u dodatnich:

	1
u +		≥ 2
	u

łatwe do udowodnienia metodami elementarnymi (bez pochodnej) i jego odpowiednik dla u ujemnych .