Pochodne N3xT:

	lnx:
f(x)=
	x2

Oblicz monotonicznos i ekstrema lokalne funkcji. Dziedzina to x∊(−∞,0)(0,∞)

Janek191: D = ( − ∞, 0) ∪ ( 0, +∞) = ℛ \{0|

N3xT: no tak a pochodną jak policzyć i potem przyrównać do 0 skoro tam jest ln

N3xT: ?

Janek191: Zastosuj wzór na pochodna ilorazu funkcji

N3xT:

x−2lnx
	'
x4

Janek191: Nie

	1 − 2 ln x
f '(x) =
	x3

Janek191:

	1x*x2 − ln x* 2 x		x − 2 x* ln x		1 − 2 ln x
f '(x) =		=		=
	x4		x4		x3

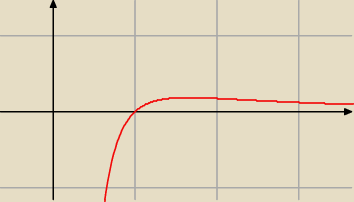
Janek191: Ze względu na ln dziedzina D = ( 0 : +∞)

Janek191: f '(x) = 0 ⇔ 1 − 2 ln x = 0 ⇔ 2 ln x = 1 ⇔ ln x = 0,5 ⇔ x = e^0,5 = √e ≈ 1,65

Janek191: Dla x < √e jest f '(x) > 0 − funkcja rośnie Dla x > √e jest f '(x) < 0 − funkcja maleje W x = √x funkcja f osiąga maksimum równe f( √e)

zyx: to ln=e ? czemu tak

	1
lnx=
	2

x=e^0,5 ?

Jerzy: a o co konkretnie pytasz ?

zyx: no skąd to e się wzięło ? skoro mam Ln ? jak to jest proszę mam kolosa w weekend z tego −,− Wytłumaczcie f(x)=ln³x−3ln²x+2 − jak to ruszyć ?

Jerzy: a co masz z tym zrobić ?

zyx: to samo co wyżej ?

zyx: a i dlaczego liczymy fmax ? a nie min ? skoro mi tu min wychodzi

Jerzy: 1) ustal dziedzinę 2) liczymy pochodną ... potrafisz ?

zyx: czekaj policzę

zyx: no dziedzina to D(f):x∊R ale pochodnej to nie wiem co z tymi potęgami przy ln

Jerzy: D = (0,+∞) [ logarytm istnieje tylko dla liczb dodatnich ] wskazówka do pochodnej: [(f(x))ⁿ]' = n*[f(x)]ⁿ⁻¹*f'(x)

zyx: wychodzi mi coś takiego :

3(lnx)2		4lnx
	−		?
x		x

zyx: i teraz x możemy przed nawias wyciągnąć ? i się skróci ? tak ?

zyx: 3lnx−4ln ? tak ?

Jerzy:

	3ln2x − 6lnx		3lnx(lnx − 2)
prawie dobrze ... f'(x) =		=
	x		x

teraz szukamy miejsc zerowych pochodnej

Jerzy: nic się nie skraca

zyx: czemu 6lnx ? mi wychodzi 4

	1
2ln2x= 2[(lnx)2] ' *		?
	x

czyli = 4lnx/x ?

Jerzy:

	1		6lnx
[3ln2x]' = 3*2*lnx*		=
	x		x

zyx: czyli mz to x=e i x=e² ?

Jerzy: a dlaczego x = e ?

zyx: 3lnx=0 lnx=0

Jerzy: lnx = 0 ⇔ x = 1

Janek191: Do 9.58 ln x = 0,5 log_e x = 0,5 ⇔ x =e^0,5 = √e ( Definicja logarytmu )

zyx: czemu ? tak czemu przecież 3lnx=0/3 lnx=0 skąd ta 1 ?

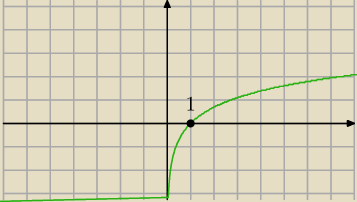
Jerzy: y = lnx teraz widzisz ?

Jerzy: albo: lnx = 0 ⇔ lnx = lne⁰ ⇔ lnx = ln1 ⇔ x = 1

zyx: no dobrze widzę a co z tym lnx−2 ? to wyjdzie e² ?

Jerzy: tak .... teraz trzeba ustalić czy i jak pochodna zmienia znak w x = 1 i x = e²

Janek191: Wydaje się,że zyx: nie zna definicji logarytmu

zyx: czyli ? No przechodzi przez 1 i przez e² ? i od prawej od góry ?

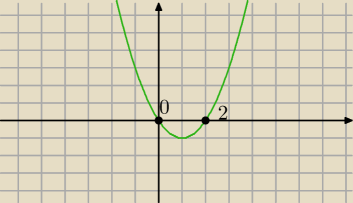
Jerzy: spokojnie ... zauważ,że znak pochodnej zależy tylko od wyrażenia lnx(lnx − 2) , bo mianownik jest zawsze dodatni podstawmy: lnx = t , czyli badamy znak funkcji: f(t) = t*(t − 2) patrz na wykres i odczytuj

zyx: a co z punktem 1 ? x=1 ?

Jerzy: dobra , szkoda czasu , to jest wykres fragmentu pochodnej , a nie funkcji w t = 0 ( dla x = 1) pochodna zmienia znak z dodatniego na ujemny, czyli funkcja ma maksimum. w t = 2 ( dla x = e² ) pochodna zmienia znak z ujemnego na dodatni, czyli funkcja ma minimum

zyx: ale spokojnie już zajazyłem jest rosnąca (−∞,0)u(2,∞) i malejąca od (0,2) i max ma w 0 a min w 2 spokojnie po prostu potrzebuje czasu

Jerzy: nie myl pojęć ... mówimy teraz już o funkcji, a nie pochodnej, a ta ma maksimum dla x = 1 oraz minimum dla x = e²