pliss o szybkie rozwiązanie pipi: Wyznacz równania osi symetrii o odcinka AB. a) A ( −7,3) B ( 5,3) b) A ( −2,−3) B ( 0 , 3) c) A( −2 , −10) B (4 , 8 )

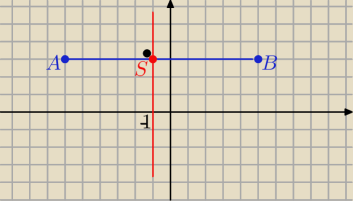
Eta: a) oś symetrii ma równanie x= −1

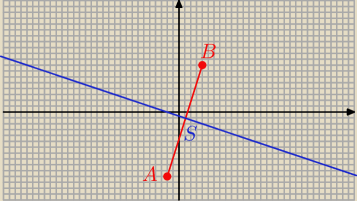
Janek191: c) A =( − 2; − 10) B = ( 4, 8)

	8 − (−10)		18
a =		=		= 3
	4 − (−2)		6

	1
a1 = −
	3

S = − środek odcinka AB

	− 2 + 4		− 10 +8
xs =		= 1 ys =		= − 1
	2		2

S = ( 1 ; − 1) więc

	1
y = −		x + b
	3

	1
− 1 = −		*1 + b
	3

	1		2
b = − 1 +		= −
	3		3

Odp.

	1		2
y = −		x −
	3		3

=================

Eta: 2 sposób b) |AC|=BC| , C(x,y) ∊ symetralnej (x+2)²+(y+3)²=(x+0)²+(y−3)² x²+4x+4+y²+6y+9=x²+y²−6y+9 4x+12y+4=0 /:4 x+3y+1=0 −−−− równanie symetralnej

pipi: Dziękuję

Eta: c) |AC|=|BC| (x+2)²+(y+10)²=(x−4)²+(y−8)² x²+4x+4+y²+20y+100=x²−8x+16+y²−16y+64 12x+36y+24=0 /:12 ⇒ x+3y+2=0 −−− równanie symetralnej w postaci ogólnej lub w postaci kierunkowej ( jaką podał Janek

	1		2
y= −		x−
	3		3

pipi: Dzięki

Janek191: