ciagłość funkcji dzialo11: Witam może ktoś zrobić 3 zadanie ? ważne mam kolosa o 16 http://www110.zippyshare.com/v/NYWk3edf/file.html

Benny:

	π
f(		)=limx→π/2−(ax+1)=limx→π/2+sinx+b
	2

	π		aπ
f(		)=		+1
	2		2

	aπ
limx→π/2−(ax+1)=		+1
	2

lim_x→π/2⁺sinx+b=1+b

dzialo11: te dwa limesy mają być równe ?

Benny: Tak

dzialo11: benny wrzuciłem inną grupę mógłbyś ją zrobić ? dzięki

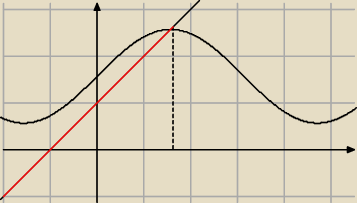Janek191: a x + 1 dla x ≤ 0,5 π f(x) = sin x + b dla x > 0,5 π f( 0,5π ) = 0,5 π*a + 1 lim ( sin x + b) = 1 + b = 0,5 a + 1 x→ 0,5π⁺ 0,5 aπ + 1 = 1 + b b = 0,5π a ; gdzie a ∊ ℛ