algebra Filip: Obliczyć pierwiastek z −i 3 stopnia. Wynik podać w postaci algebraicznej, trygonometrycznej i wykładniczej . Pomocy , z gory dziekuje

Janek191:

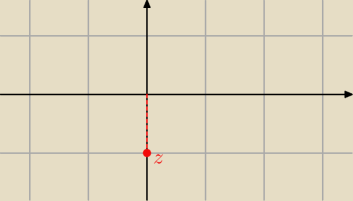
	3π		3π
z = − i = cos		− i sin		= cos 270o − i sin 270o
	2		2

I z I = 1 k ∊ { 0,1,2}

	270o + 360o		270o + 369o
z0 = cos		+ i sin		= cos 210o + i sin 210o =
	3		3

	√3		1
= − cos 30o − i sin 30o = −		−		i
	2		2

	270o + 2*360o		270o + 720o
z1 = cos		+ i sin		= cos 330o + i sin 330o =
	3		3

	√3		1
= sin 60o − i cos 60o =		−		i
	2		2

Filip: Dzięki wielkie Janek191 !

Janek191: Pomyłka

	270 + 0*360p		270o + 0*360o
z0 = cos		+ i sin		= cos 90o + i sin 90o = 0 + i
	3		3

	270 +1*360o		270o + 1*360o		√3		1
z1 = cos		+ i sin		= −		−		i
	3		3		2		2

	270o + 2*360o		270o +2*360o		√3		1
z2 = cos		+ i sin		=		−		i
	3		3		2		2

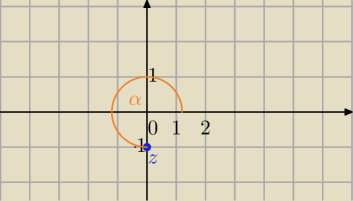Mila: z=−i |z|=1

	3π
α=
	2

	α+2kπ		α+2kπ
zk=3√|z|*(cos(		)+i sin(		)), gdzie k=0,1,2
	3		3

	π		π
z0=cos(		+i sin		=i
	2		2

	3π   +2π 2		3π   +2π 2		7π		7π
z1=(cos		+i sin		)=(cos		+i sin		)=...
	3		3		6		6

licz dalej sam