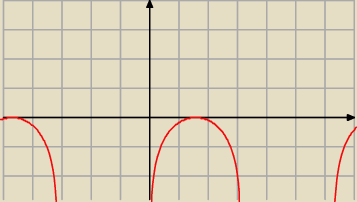
Zbadaj funkcję ln(sinx) Ania21: Cześć, potrzebuję zrobić zadanie, z którym zupełnie nie mogę sobie poradzić.Mam zbadać funkcję ln(sinx). Muszę wykonać następujące punkty: 1)dziedzina 2)m. zerowe 3)monotoniczność 4)ekstrema 5)asymptoty 6)punkty przegięcia 7)wypukłość, wklęsłość 8)wykres

Janek191: 1) sin x > 0 ⇔ x ∊ ( 0 + 2π*k ; π + 2π*k ) , gdzie k − dowolna liczba całkowita

Janek191: 2)

	π
ln ( sin x) = 0 ⇔ sin x = e0 = 1 ⇔ x =		+ 2π*k
	2

Ania21: można prosić o dalszą część

Janek191:

	cos x
3) f '(x) =		=ctg x
	sin x

	π
f '(x) > 0 ⇔ x ∊ ( 0 + 2π*k ;		+ 2π*k − wtedy funkcja rośnie
	2

	π
f '(x) < 0 ⇔ x ∊ (		+ 2π*k , π +2 π* k) − wtedy funkcja maleje
	2

4)

	π
f '(x) = 0 ⇔ ctg x = 0 ⇔ x =		+ 2π*k
	2

Wtedy funkcja f ma maksimum lokalne y_max = 0

Ania21: dziękuję bardzo, brakuje mi jeszcze asymptot i wypukłości i wklęsłości.