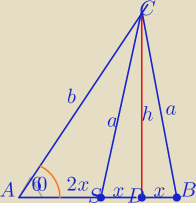
 SC − środkowa, ΔCSB− trójkąt równoramienny.
SC − środkowa, ΔCSB− trójkąt równoramienny.
| 1 | ||
|AD|= | b | |
| 2 |
| 1 | ||
3x= | b | |
| 2 |
| 1 | ||
x= | b | |
| 6 |
| 2 | ||
AB= | b | |
| 3 |
| 2 | 2 | |||
a2=b2+( | b)2−2*b** | b*cos60o | ||
| 3 | 3 |
| 7 | ||
a2= | b2 | |
| 9 |
| 3a | 3a√7 | |||
b= | = | |||
| √7 | 7 |
| 2 | 3a√7 | |||
|AB|= | * | |||
| 3 | 7 |
| 2a√7 | ||
|AB|= | ||
| 7 |


 Przepraszam, ale nie zrozumiałam treści
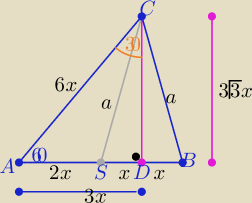
Przepraszam, ale nie zrozumiałam treści  Na poziomie gimnazjum ( z trójkąta ADC .. "ekierki" o kątach 30o, 60o, 90o
|AD|=3x , AC|=6x, |CD|=3√3x , x>0 , |SD|=x
z twierdzenia Pitagorasa w ΔSDC :
Na poziomie gimnazjum ( z trójkąta ADC .. "ekierki" o kątach 30o, 60o, 90o
|AD|=3x , AC|=6x, |CD|=3√3x , x>0 , |SD|=x
z twierdzenia Pitagorasa w ΔSDC :
| a | ||
x2+27x2=a2 ⇒ a2=28x2 ⇒ x= | ||
| 2√7 |
| 3a | 3a√7 | 2a√7 | ||||
to: |AC|= | = | , |AB|=4x= | ||||
| √7 | 7 | 7 |