Proste
math: Trzy punkty A,B,C leżące na paraboli y=x2−4 są wierzchołkami trójkąta, przy czym C leży na tej
krzywej pomiędzy punktami A i B. Punkty A i B należą do prostej y=−2x−1. Wyznacz współrzędne
punktów A,B,C wiedząc, że pole trójkąta ABC jest maksymalne.
Prosiłbym o pomoc. Po narysowaniu i znalezieniu punktów wspólnych prostej z parabolą,
wyznaczyłem punkty A i B, natomiast nie wiem jak wyznaczyć punkt C.
17 sty 18:24
===:
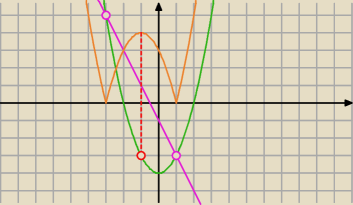
17 sty 19:31
Janek191:
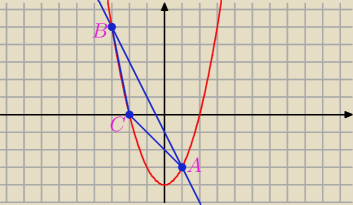
A = ( 1; −3) B = ( 3, 5 )
C = ( x ; x
2 − 4)
→
CA = [ 1 − x, − 3 − x
2 + 4 ] = [ 1 − x; 1 − x
2 ]
→
CB = [ 3 − x, 5 − x
2 + 4 ] = [ 3 − x, 9 − x
2 ]
Wzór na pole Δ
ABC
→ →
P = 0, 5 I det (CA , CB ) = 0,5 I ( 1− x)*(3 − x) + ( 1 − x
2)*( 9 − x
2) I =
= 0,5 I 3 − x − 3x + x
2 + 9 − x
2 − 9 x
2 + x
4 I = 0,5 I x
4 − 9 x
2 − 4 x + 12 I =
= 0,5 I ( x
2 − 4 x + 3)*(x
2 + 4 x + 4) I = 0,5 I ( x − 3)*(x − 1)*(x + 2)
2 I
x ∊ ( − 3 , 1), więc
P = 0,5 *( 3 − x)*( 1 − x)*( x + 2)
2
P = 0, 5*( x
2 − 4 x + 3)*(x + 2)
2
P ' = 0,5 [ (2 x − 4)*(x + 2)
2 + ( x
2 − 4 x + 3)*( 2x + 4)] =
= ( x − 2)*( x + 2)
2 +( x + 2)*(x
2 − 4 x + 3) = 0 ⇔ x = − 2
Wtedy C = ( − 2, 0 )
===============
17 sty 19:38
Janek191:
Gdzieś się pomyliłem

17 sty 19:41
===:
Wyznacz punkty przecięcia się prostej i paraboli aby określić położenie punktu C
(−3<x
c<1)
C=(x
c, x
x2−4)
Pole trójkąta ABC będzie max dla maksymalnej wysokości tj.odległości punktu C
pd prostej 2x+y+1=0
Dalej dla Ciebie

17 sty 19:43
===:
i szukasz max dla |x
c2+2x
c−3| ... w określonym wcześniej przedziale dla x
c 
17 sty 19:47
math: Tak, ale to wtedy nie wyjdą miejsca zerowe x1=−3, x2=1 ? Z tego co mi wiadomo, ten punkt
powinien wyjść (−1, −3 ).
17 sty 19:56
Janek191:
Tak wyszło u ===;
17 sty 20:05
math: Tzn, ale jak to policzyć? bo nie rozumiem jak znaleźć max dla tej wartości bezwzględnej. Czyżby
pochodna?
17 sty 20:08
===:
Maturzysta wykres funkcji g(x)=|x
2+2x−3| sporządzić chyba potrafi
i wartość największą w danym przedziale też określić umie

17 sty 20:14
Jack: a umie, dziekowac

17 sty 20:22
===:
jak widać NIE

17 sty 20:55

 A = ( 1; −3) B = ( 3, 5 )
C = ( x ; x2 − 4)
→
CA = [ 1 − x, − 3 − x2 + 4 ] = [ 1 − x; 1 − x2 ]
→
CB = [ 3 − x, 5 − x2 + 4 ] = [ 3 − x, 9 − x2 ]
Wzór na pole ΔABC
→ →
P = 0, 5 I det (CA , CB ) = 0,5 I ( 1− x)*(3 − x) + ( 1 − x2)*( 9 − x2) I =
= 0,5 I 3 − x − 3x + x2 + 9 − x2 − 9 x2 + x4 I = 0,5 I x4 − 9 x2 − 4 x + 12 I =
= 0,5 I ( x2 − 4 x + 3)*(x2 + 4 x + 4) I = 0,5 I ( x − 3)*(x − 1)*(x + 2)2 I
x ∊ ( − 3 , 1), więc
P = 0,5 *( 3 − x)*( 1 − x)*( x + 2)2
P = 0, 5*( x2 − 4 x + 3)*(x + 2)2
P ' = 0,5 [ (2 x − 4)*(x + 2)2 + ( x2 − 4 x + 3)*( 2x + 4)] =
= ( x − 2)*( x + 2)2 +( x + 2)*(x2 − 4 x + 3) = 0 ⇔ x = − 2
Wtedy C = ( − 2, 0 )
===============
A = ( 1; −3) B = ( 3, 5 )
C = ( x ; x2 − 4)
→
CA = [ 1 − x, − 3 − x2 + 4 ] = [ 1 − x; 1 − x2 ]
→
CB = [ 3 − x, 5 − x2 + 4 ] = [ 3 − x, 9 − x2 ]
Wzór na pole ΔABC
→ →
P = 0, 5 I det (CA , CB ) = 0,5 I ( 1− x)*(3 − x) + ( 1 − x2)*( 9 − x2) I =
= 0,5 I 3 − x − 3x + x2 + 9 − x2 − 9 x2 + x4 I = 0,5 I x4 − 9 x2 − 4 x + 12 I =
= 0,5 I ( x2 − 4 x + 3)*(x2 + 4 x + 4) I = 0,5 I ( x − 3)*(x − 1)*(x + 2)2 I
x ∊ ( − 3 , 1), więc
P = 0,5 *( 3 − x)*( 1 − x)*( x + 2)2
P = 0, 5*( x2 − 4 x + 3)*(x + 2)2
P ' = 0,5 [ (2 x − 4)*(x + 2)2 + ( x2 − 4 x + 3)*( 2x + 4)] =
= ( x − 2)*( x + 2)2 +( x + 2)*(x2 − 4 x + 3) = 0 ⇔ x = − 2
Wtedy C = ( − 2, 0 )
===============





